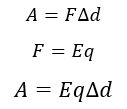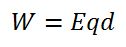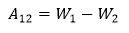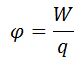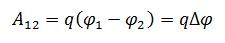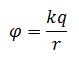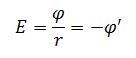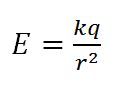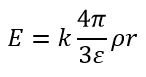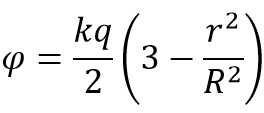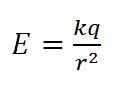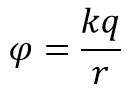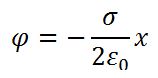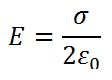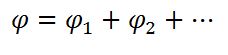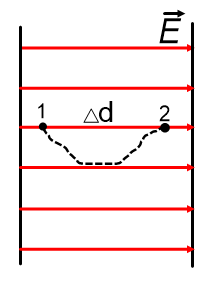
При перемещении заряда в однородном электрическом поле с напряженностью Е из точки 1 в точку 2 любую траекторию можно представить в виде ломанной линии со сколь угодно малыми ступеньками параллельными линиям напряженности и перпендикулярными им. В направлении, перпендикулярном линиям напряженности, работу электрическое поле не совершает.
Поле, в котором работа сил не зависит от формы траектории, а по замкнутой траектории равна нулю, называется потенциальным.
Потенциальная энергия заряда в электрическом поле
Работа электрического поля по перемещению заряда из точки 1 в точку 2 равна разности потенциальных энергий в этих точках.
Энергетическая характеристика электрического поля
|
Потенциал – это физическая величина, равная отношению потенциальной энергии заряда в электрическом поле к этому заряду |
Тогда работу электрического поля можно выразить через разность потенциалов:
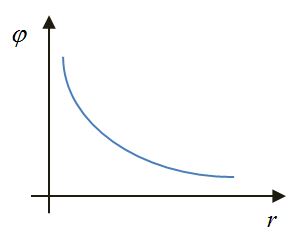
Потенциал электрического поля точечного заряда на расстоянии r от него
Связь потенциала и напряженности:
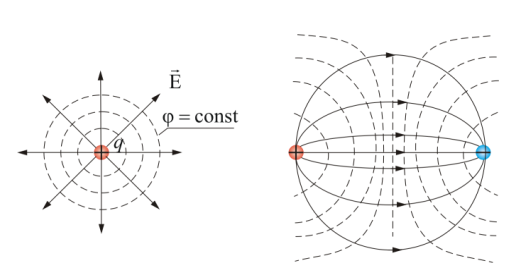
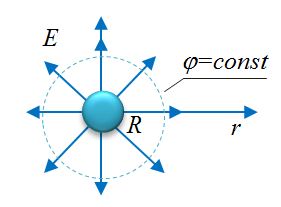
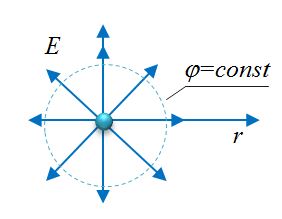
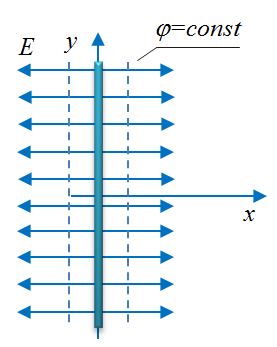
Поверхности равного потенциала (эквипотенциальные поверхности) – геометрическое место точек, имеющих одинаковый потенциал.
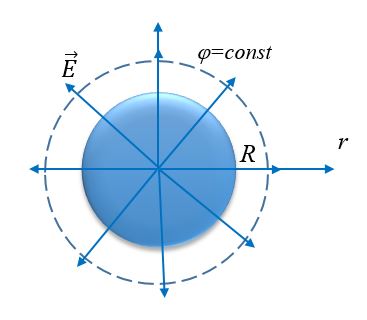
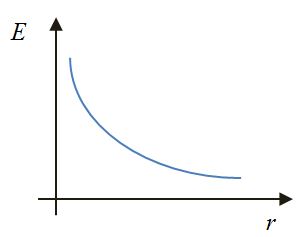
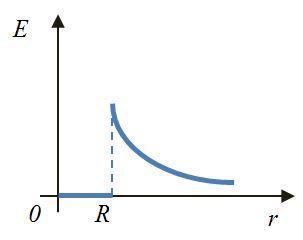
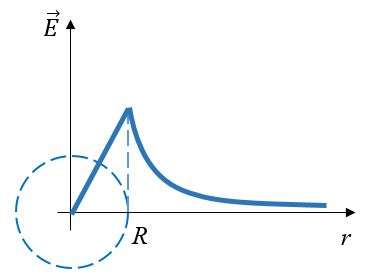
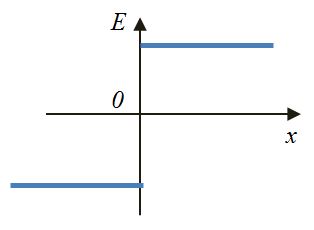
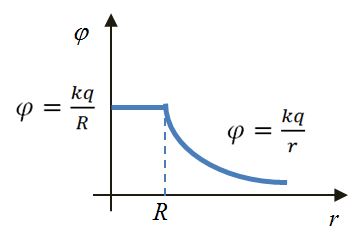
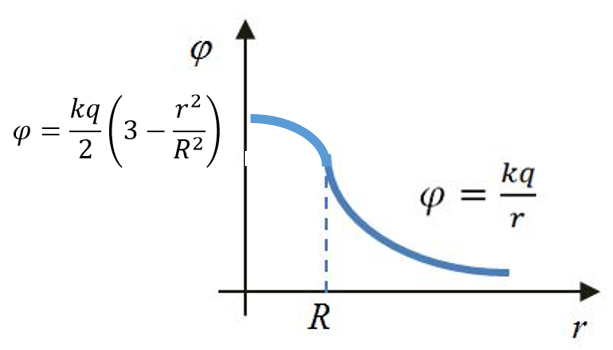
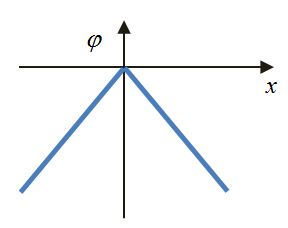
| Точечный заряд | Сфера | Шар | Плоскость |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
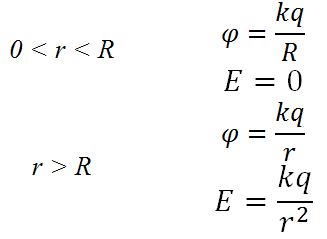 |
При r < R
при r >= R
|
|
Принцип суперпозиции полей: если в точке пространства существует несколько электрических полей, то потенциал суммарного поля в данной точке равен алгебраической сумме потенциалов всех полей (с учетом знака):