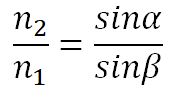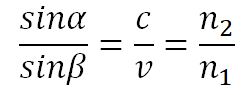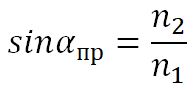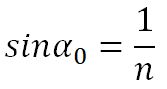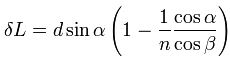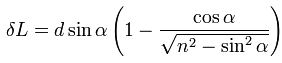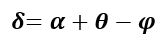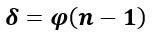Принцип Гюйгенса:
Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
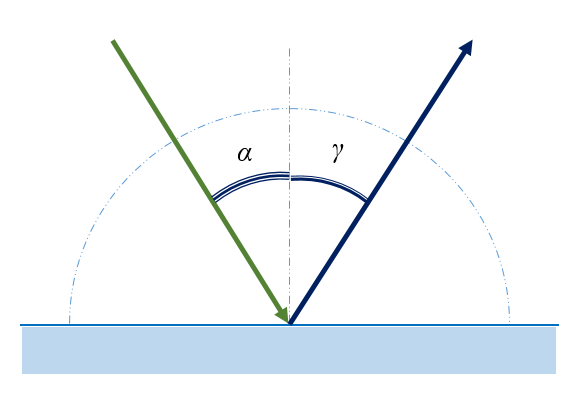
Закон отражения:
- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
- угол падения α равен углу отражения γ:
α = γ
Вывод на основе принципа Гюйгенса:
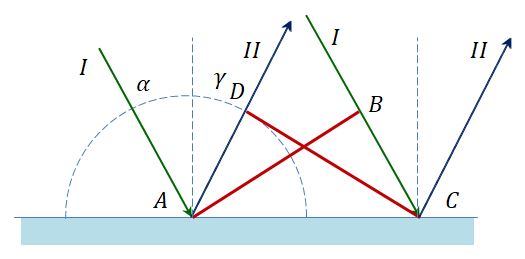
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
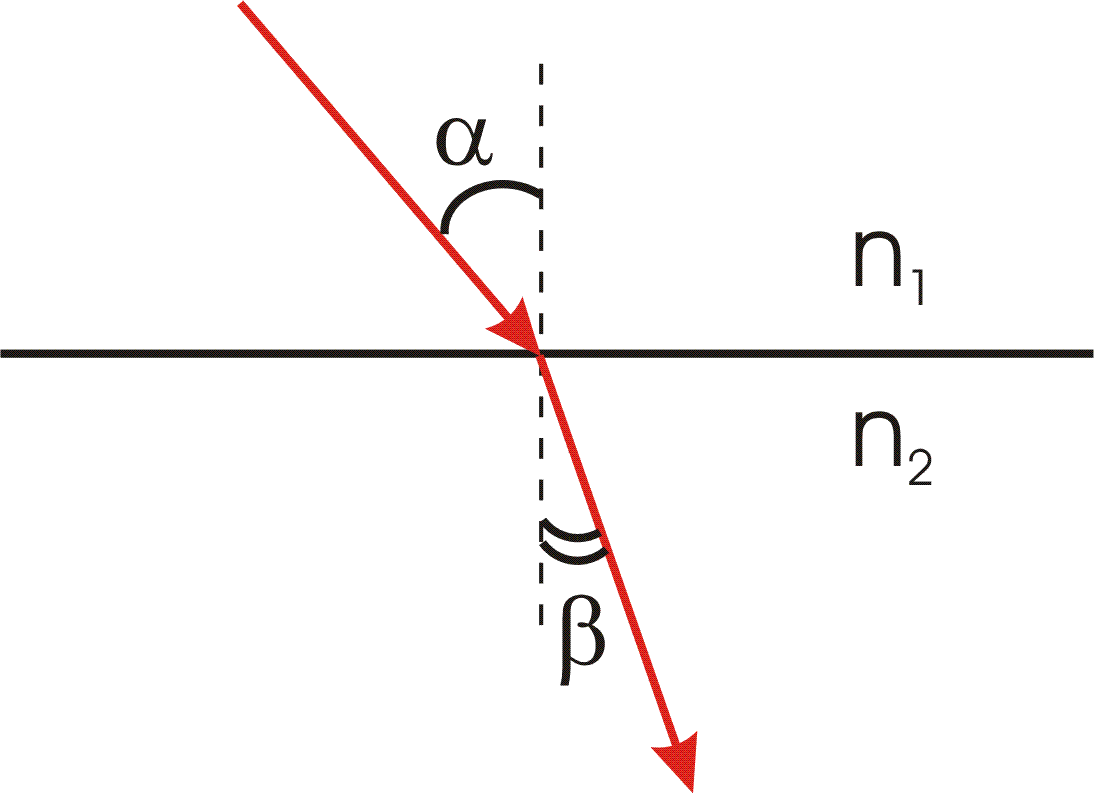
Закон преломления (закон Снелиуса):
- луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
- отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.

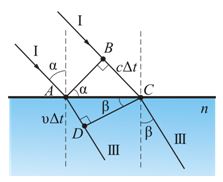
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.
Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что
 , т.е.
, т.е.  .
.
Отсюда следует закон Снелиуса:
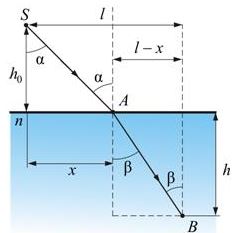
Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.
Покажем применение этого принципа к решению той же задачи о преломлении света.
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:
 .
.
Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:
 ,
,
отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса:  .
.
Следствия из принципа Ферма:
1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.
2. Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотной) ( n1 > n2 ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:
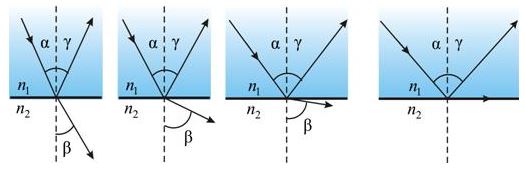
3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = αпр) угол преломления не окажется равным π/2.
Полное отражение
Угол αпр называется предельным углом полного отражения. При углах падения α > αпр весь падающий свет полностью отражается.
По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.
Если α = αпр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.
Таким образом, при углах падения в пределах от αпр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
В случае, если вторая среда - воздух

Преломление света в плоскопараллельной пластине
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча
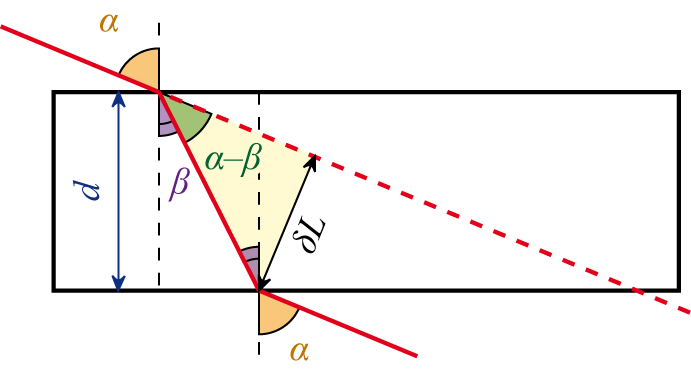
Величина смещения в плоскопараллельной пластине
Величина сдвига луча света δL зависит:
- от угла падения света α,
- от толщины пластины d,
- от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.
C увеличением любого из этих параметров смещение луча света увеличивается.
Смещение луча можно выразить через угол падения
Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:
- угол падения равен нулю: α = 0,
- относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
- толщина пластины равна нулю: d = 0
Ход луча через треугольную призму
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.
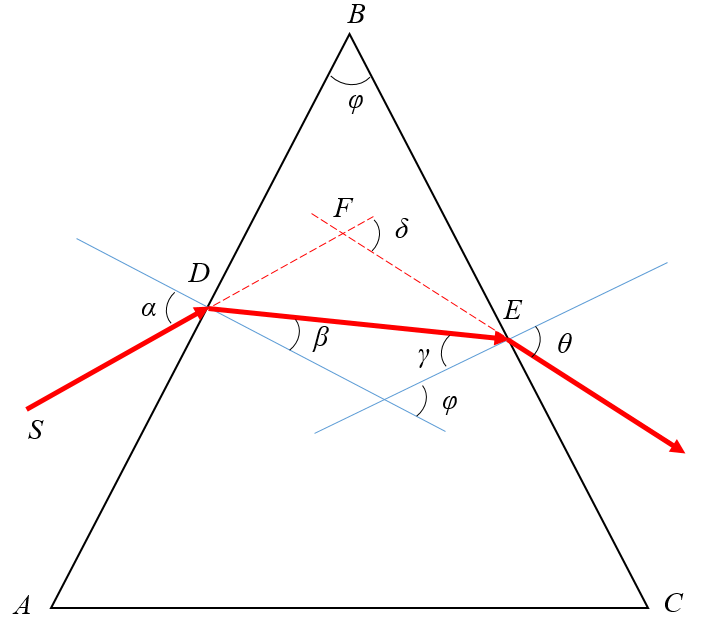
На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.
Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой
Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.
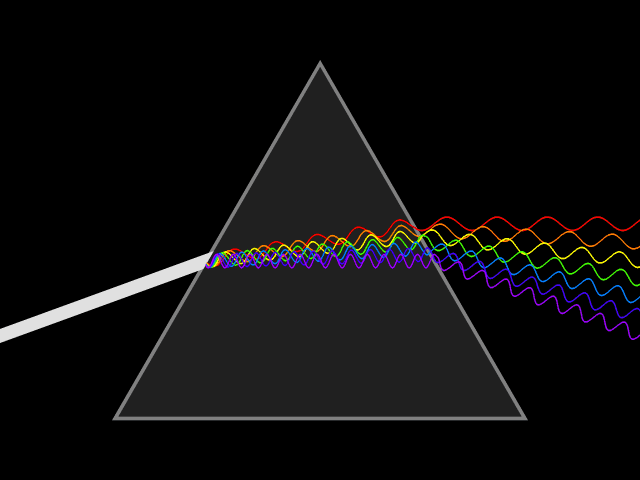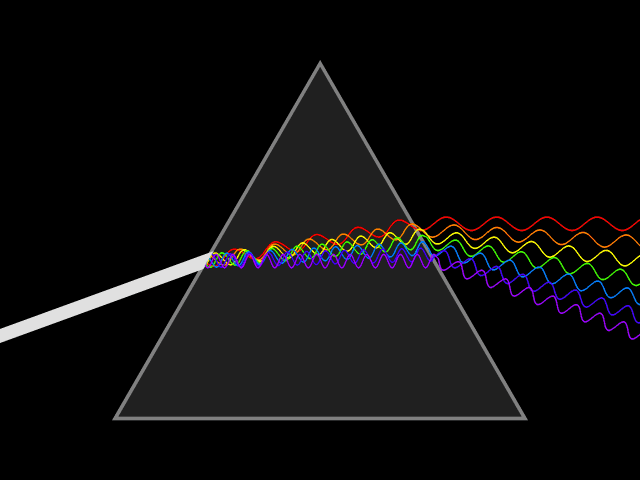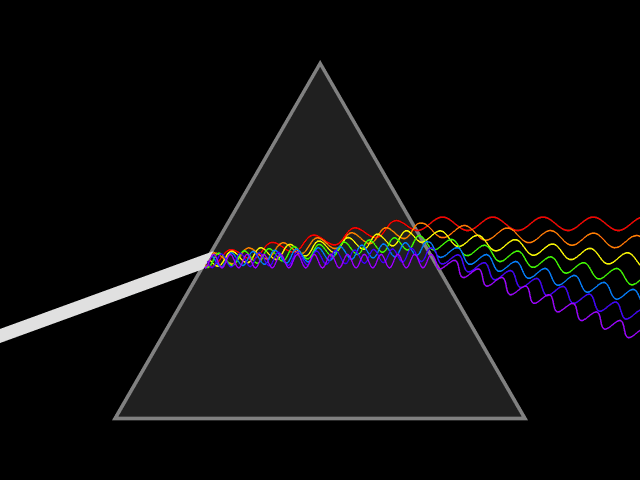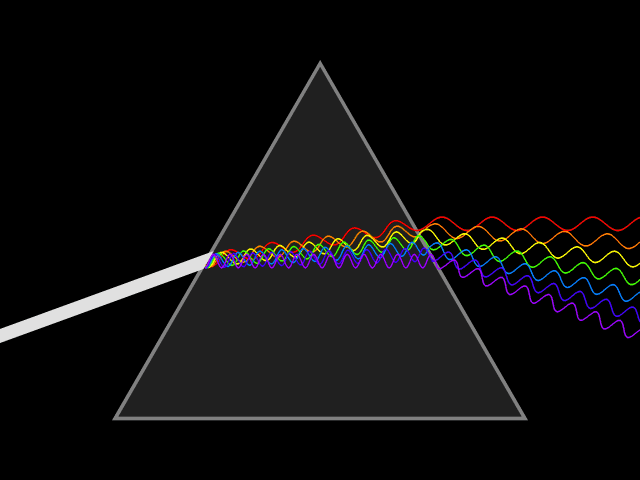
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.