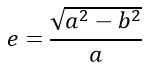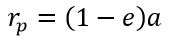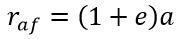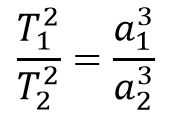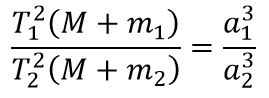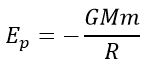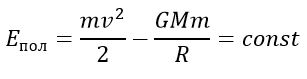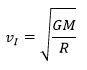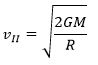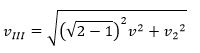Первый закон Кеплера (закон эллипсов)
| Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. |
Форма эллипса и степень его сходства с окружностью характеризуется отношением
или e = c/a,
где c - расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a - большая полуось, b - малая полуось. Величина eназывается эксцентриситетом эллипса. При c = 0, и, следовательно, e = 0,эллипс превращается в окружность. В случае тонкого длинного эллипса е стремится к 1.
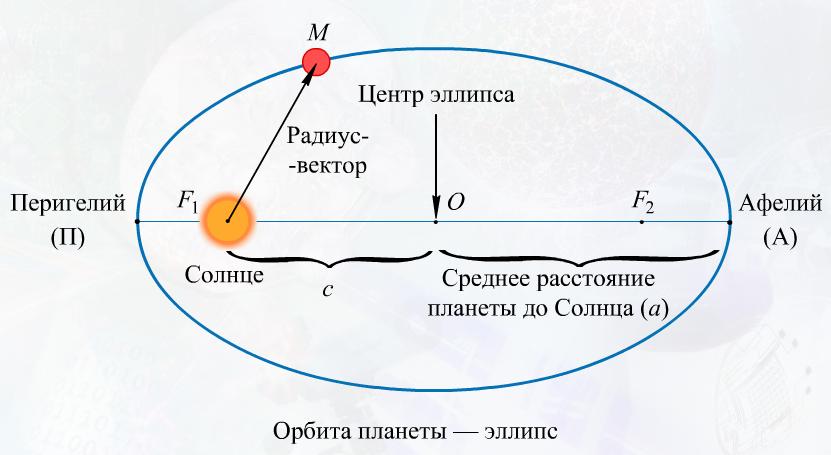
Перигелий - ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.
Афелий - наиболее удаленная точка орбиты.
где a — большая полуось, е — эксцентриситет орбиты.
Современная формулировка распространяет действие закона на любые гравитационно-связанные системы тел:
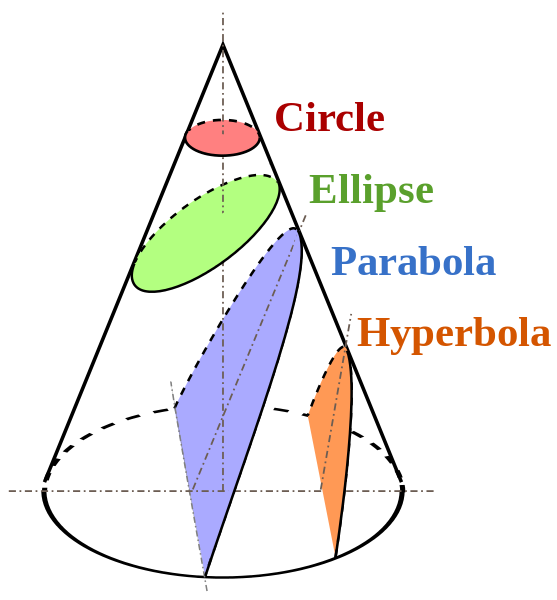
В гравитационно-связанной системе тело B движется по эллипсу, в одном из фокусов которого находится тело A. Эксцентриситет эллипса определяется численным значением полной энергии системы. В гравитационно-несвязанной системе тело B движется по параболе (E= 0) или по гиперболе (E > 0), в фокусах которых находится тело A.
Доказательство связано с тем, что под действием гравитационной силы тела могут двигаться только по коническим сечениям – окружности, эллипсу, параболе или гиперболе.
Второй закон Кеплера (закон площадей)
| Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. |
Из закона следует, что планета движется по орбите неравномерно, быстрее в перигелии (ближайшей к Солнцу точке) и медленнее в афелии (наиболее удаленной точке).
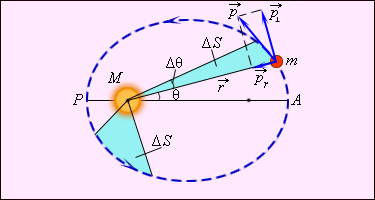
Доказательство закона связано с постоянством момента импульса планеты как материальной точки.
Третий закон Кеплера (гармонический закон)
| Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. |
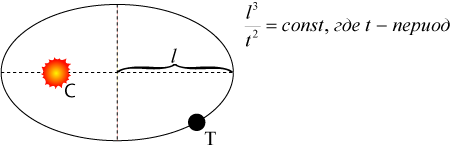
В формулировке Ньютона в закон входят и массы звезды и планеты:
Этот закон позволяет определить массы планет и спутников из известных орбит и периодов обращения.
Доказательство проводится на основе закона всемирного тяготения Ньютона.
Применение законов Кеплера
Потенциальная энергия взаимодействия двух тел
Пусть два тела с массами M и m находятся на расстоянии R друг от друга. Тогда энергия их взаимодействия равна
Полная энергия
Если тело находится в гравитационном поле и имеет некоторую скорость, то его полная энергия равна
Таким образом, в соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.
Теорема вириала
В случае кругового движения кинетическая энергия в 2 раза меньше по модулю потенциальной. Поэтому
2Eк+Eп= 0
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела.
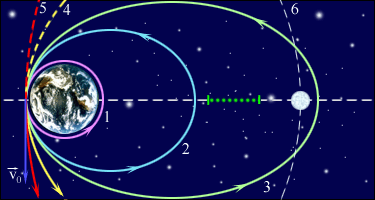
При Eпол < 0 тело не может удалиться от центра притяжения на расстояние r0 < rmax . В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы). Система с отрицательной полной энергией называется гравитационно связанной.
При Eпол = 0 тело движется по параболической траектории. Скорость тела на бесконечности равна нулю.
При Eпол > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.
Первая космическая скорость
Это скорость движения по круговой траектории вблизи поверхности Земли
Это минимальная скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и стало спутником. Для Земли примерно 7,9 км/с.
Вторая космическая скорость
Это скорость движения по параболической траектории
Она равна минимальной скорости, которую нужно сообщить телу на поверхности Земли, чтобы оно, преодолев земное притяжение, стало искусственным спутником Солнца. Находится из условия равенства нулю полной энергии системы. Для Земли примерно 11,2 км/с.
Третья космическая скорость
Это скорость, при которой тело преодолевает притяжение Солнца
где v – орбитальная скорость планеты, v2 – вторая космическая скорость для планеты. Для Земли примерно 16,6 км/с.
Задачи:
Звезда и планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите массу планеты m, если известно, что скорость движения планеты равна v1, а скорость движения и период обращения звезды равны v2 и T соответственно.
Если бы все линейные размеры Солнечной системы были пропорционально сокращены так, чтобы среднее расстояние между Солнцем и Землей стало 1 м, то какова была бы продолжительность одного года? Считайте, что плотность небесных тел при этом не меняется.
Автоматическая станция обращается вокруг планеты Марс с периодом T = 18 ч. Максимальное удаление от поверхности Марса (в апоцентре) a = 25000 км, минимальное (в перицентре) p = 1380 км. По указанным параметрам орбиты станции определите отношение массы Марса к массе Земли. Радиус Марса rм = 3400 км, радиус Земли rз = 6400 км.
Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты 422 тыс. км.
Вычислить параболическую скорость на поверхности Луны, RЛ = 0.27 радиуса Земли, MЛ = 1/81 массы Земли.
Источники:
https://ru.wikipedia.org/wiki/