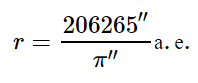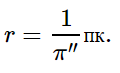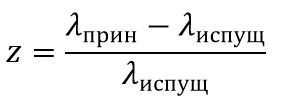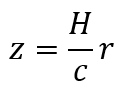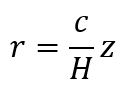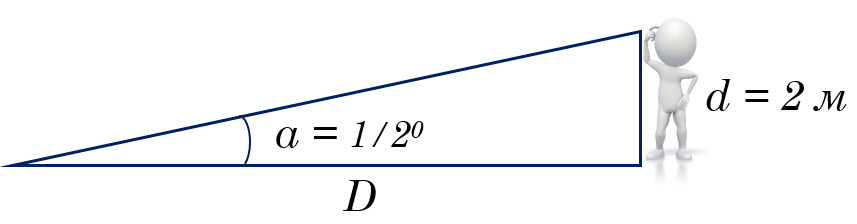Методы определения расстояний до звезд
Годичный параллакс
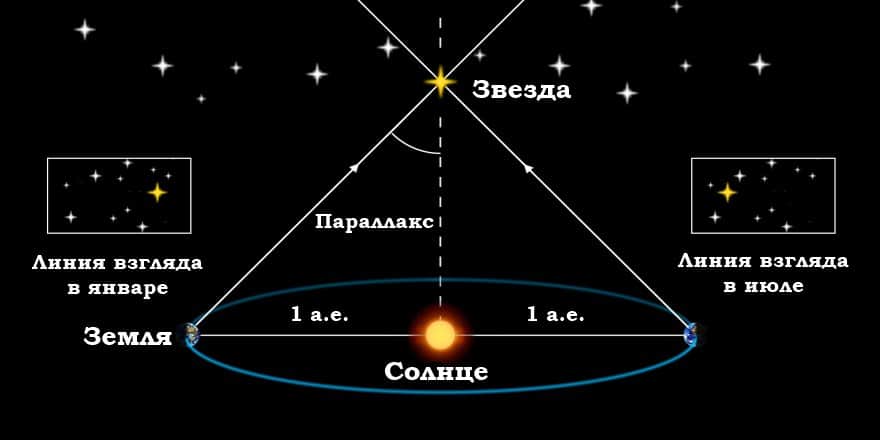
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).
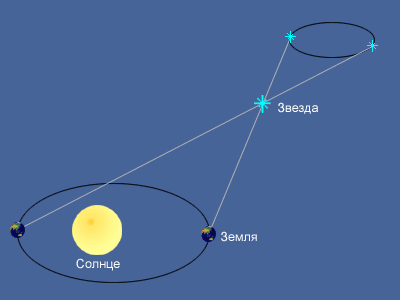
Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
Если CT = a есть средний радиус земной орбиты, SC = r - расстояние до звезды S от Солнца C, а угол π - годичный параллакс звезды, то
Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения
При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины - парсек (пк), название которой происходит от слов «параллакс» и «секунда».
Парсек - это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.
1 пк = 206 265 а. е. = 3,086 · 1013 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 103 пк) и мегапарсеках (1 Мпк = 106 пк), а также в световых годах (1 св. г. = 9,46 · 1012 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).
Световой год - расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.
Фотометрический метод определения расстояний
Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m - видимая, M - абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф(пк):
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5m. Эта погрешность соответствует относительной погрешности 30%.
Цефеиды (стандартные свечи)
Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем - галактик - основан на характерном свойстве переменных звезд - цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются. Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).
Определение внегалактических расстояний
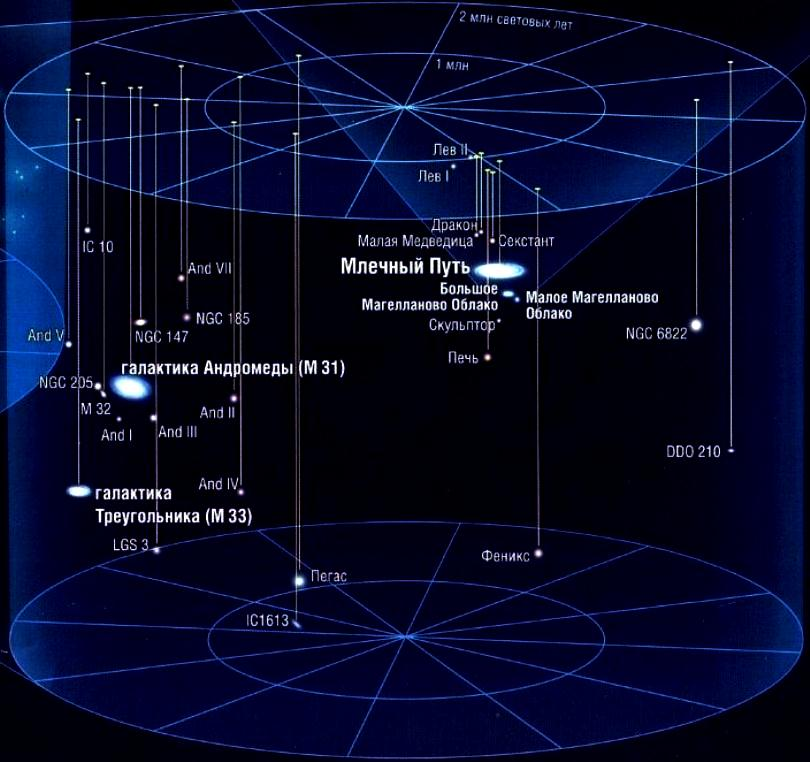
Расстояния до ближайших галактик были установлены по оценкам видимых звездных величин цефеид и ярчайших звезд в этих звездных системах. Более тысячи цефеид найдено в Магеллановых Облаках, несколько сотен - в Туманности Андромеды (М31). Цефеиды обнаружены также в семи неправильных и спиральных галактиках, находящихся в радиусе около 3 Мпк вокруг нашей Галактики.
В системах, где не удается обнаружить цефеиды, ищут ярчайшие звезды-сверхгиганты и гиганты высших классов светимости. Ярчайшие сверхгиганты обнаружены в нескольких сотнях спиральных и неправильных галактик в радиусе до 10 Мпк (абсолютные величины их - от -9 до -10m). В эллиптических галактиках население I типа (долгопериодические цефеиды, сверхгиганты и горячие газовые туманности) отсутствует. Однако небольшие эллиптические галактики нашей Местной группы на фотографиях распадаются на звезды, ярчайшие из которых оказались красными гигантами, аналогичными гигантам в шаровых звездных скоплениях нашей Галактики (абсолютные величины этих гигантов достигают -2m, радиус обнаружения - около 1 Мпк). По красным гигантам удается оценивать фотометрические расстояния до эллиптических галактик внутри Местной группы галактик с погрешностью 20%.
В качестве индикаторов расстояний используются также новые звезды и сверхновые звезды.
В некоторых галактиках наблюдаются яркие газовые туманности. Оказалось, что линейные размеры наибольших туманностей в галактиках почти одинаковы. Поэтому, измерив угловые размеры d" ярчайшей туманности в какой-либо галактике, можно определить расстояние r до этой галактики. Данный способ применим к спиральным и неправильным галактикам до расстояний 15 Мпк. Погрешность этого метода - не менее 10%.
До остальных галактик фотометрические расстояния можно определять более грубым способом по оценке интегральной звездной величины галактики. По особенностям внешнего вида спиральных галактик (толщина, длина спиральных рукавов, поверхностная яркость и т.п.) часто можно грубо оценить светимость галактики или, по крайней мере, установить, что галактика не относится к числу карликовых. В последнем случае ее абсолютную интегральную величину можно условно принять равной -20m (ср. значение для галактик-гигантов) и по видимой величине грубо оценить расстояние.
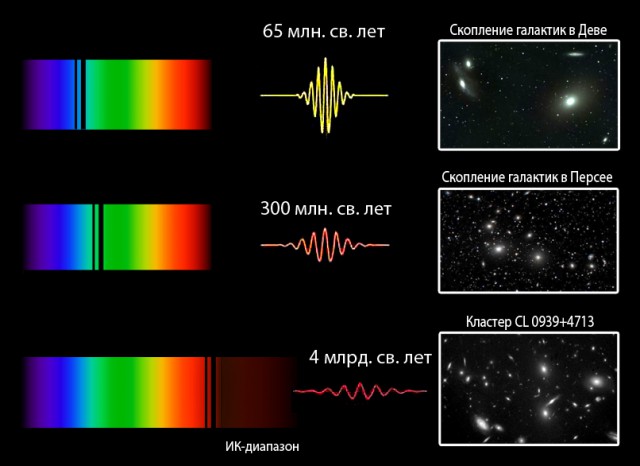
На больших расстояниях (> 1000 Мпк) видимый блеск галактик и других космических объектов ослабляется не только в силу фотометрического закона квадрата расстояния, но также, помимо поглощения света, вследствие красного смещения - "покраснения" далеких источников излучения, отражающего расширение Вселенной, что приходится учитывать при определении фотометрических расстояний.
Определение расстояний по красному смещению
Сравнение фотометрических расстояний до галактик с величиной смещения z их спектральных линий к красному концу спектра показало, что величина
пропорциональна расстоянию r (Хаббла закон):
где H - постоянная Хаббла. Отсюда получается формула для определения расстояний до далеких галактик, радиогалактик и квазаров:
- Информация о материале
- Просмотров: 35217
Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.
Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).
Уравнение малых углов
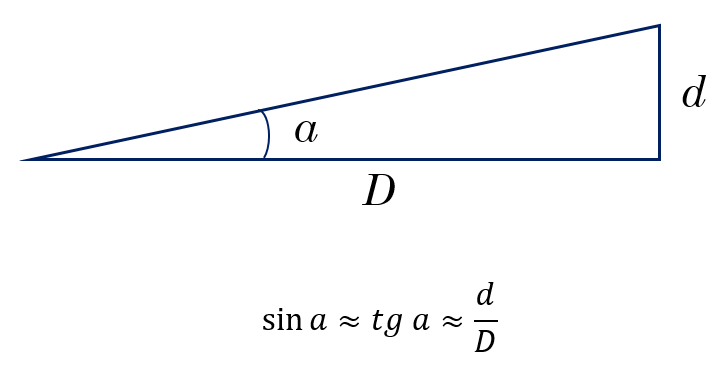
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере.
Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a, выраженному в секундах дуги. Обозначим диаметр объекта как d, а расстояние до него как D. Тогда уравнение малого угла
a / 206 265 = d / D
Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3°, который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr, Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга.
Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½°, или 1800". Как он далеко от вас? Мы хотим найти расстояние D, выразим эту величину из уранения:
D = 206 265 d / a
Используя метрические единицы, найдем
D = (2.1 x 105 x 2) / (1.8 x 103) = 2.3 х 102 метра = 230 метров
Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.
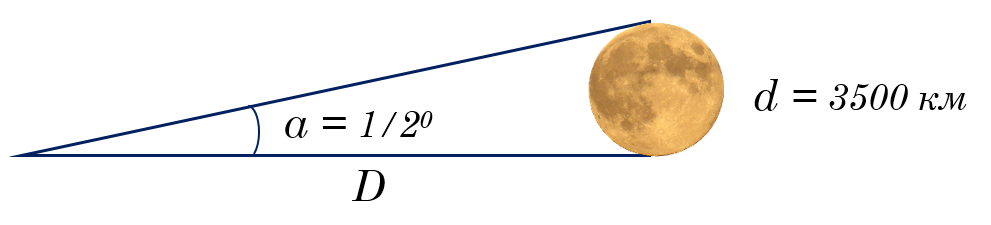
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½°, или 1800".
Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 106 метров. Уравнение будет гласить:
D = (2.1 × 105 × 3.5 × 106) / (1.8 × 103) ≈ 4 х 108 метров ≈ 4 x 105 километров.
Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!
Методы определения расстояний до звезд
Годичный параллакс
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).

Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
Если CT = a есть средний радиус земной орбиты, SC = r - расстояние до звезды S от Солнца C, а угол π - годичный параллакс звезды, то
Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения
При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины - парсек (пк), название которой происходит от слов «параллакс» и «секунда».
Парсек - это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.
1 пк = 206 265 а. е. = 3,086 · 1013 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 103 пк) и мегапарсеках (1 Мпк = 106 пк), а также в световых годах (1 св. г. = 9,46 · 1012 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).
Световой год - расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.
Фотометрический метод определения расстояний
Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m - видимая, M - абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф(пк):
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5m. Эта погрешность соответствует относительной погрешности 30%.
Цефеиды (стандартные свечи)
Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем - галактик - основан на характерном свойстве переменных звезд - цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).
- Информация о материале
- Просмотров: 29699
Смена времен года — вечное и неизменное явление природы. Причина его заключается в движении Земли вокруг Солнца.
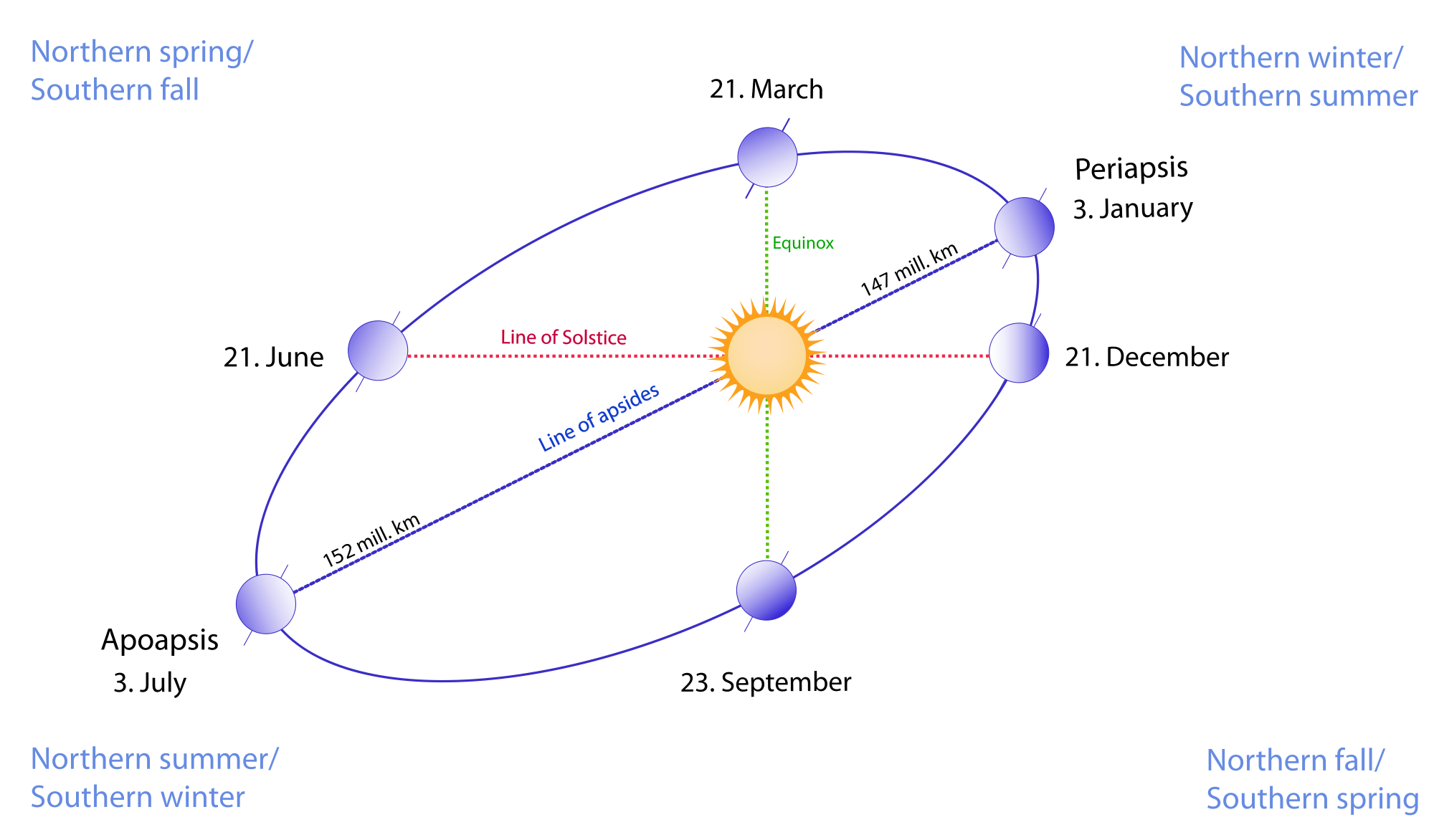
Путь, по которому в космическом пространстве движется земной шар, имеет форму вытянутого круга - эллипса. Солнце находится не в центре этого эллипса, а в одном из его фокусов. Поэтому на протяжении года расстояние от Солнца до Земли периодически меняется: от 147,1 млн. км (в начале января) до 152,1 млн. км (в начале июля). Переход от тёплого времени года (весна, лето) к холодному (осень, зима) происходит вовсе не потому, что Земля то приближается к Солнцу, то удаляется от него.
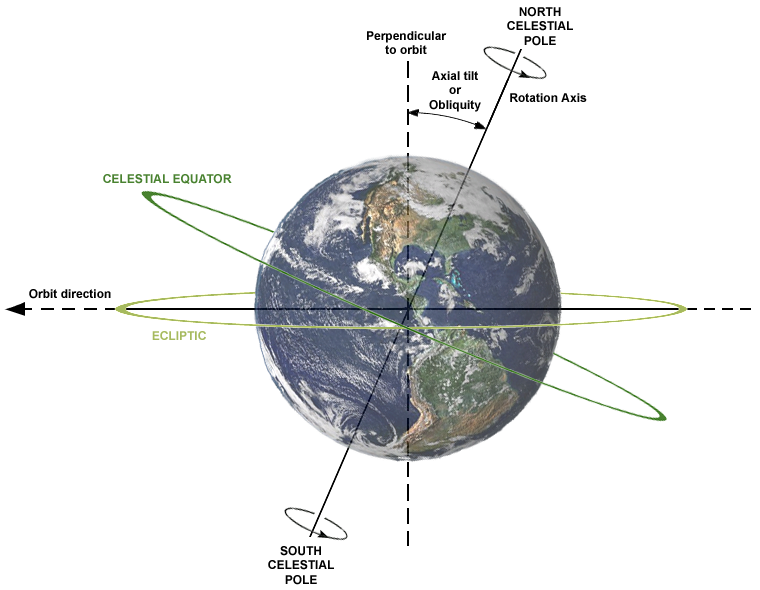
Истинная причина смены времен года — это наклон земной оси. Ось вращения, воображаемая линия, соединяющая северный и южный полюса Земли, не перпендикулярна плоскости земной орбиты, по которой она движется вокруг Солнца. И отклонение оси от перпендикуляра составляет 23,5°. Ось направлена на север в точку среди звезд возле Полярной звезды. (На самом деле, ось медленно меняет свое направление и со временем будет указывать не на Полярную, а на другую звезду.)
Лето приходит в Северное полушарие, когда ось, направленная через Северный полюс вверх, указывает примерно в сторону Солнца. В этой ситуации Солнце в полдень находится выше над горизонтом, чем во все остальные сезоны года, поэтому оно лучше освещает Северное полушарие и дает больше тепла. В это же самое время ось, проходящая вниз через Южный полюс, направлена от Солнца, поэтому Солнце в полдень находится ниже над горизонтом, чем в любое другое время года, и хуже освещает Южное полушарие. В это время в Австралии наступает зима.
Летом светлого времени суток больше, чем зимой, потому что Солнце находится выше над горизонтом. Поэтому ему требуется больше времени, чтобы сначала подняться на эту высоту, а потом — спуститься. И, поскольку день длится дольше, в это время года теплее.
По мере того как Земля движется по орбите вокруг Солнца, кажется, что Солнце перемещается по небу по некой окружности, которая называется эклиптикой. Плоскость эклиптики наклонена к плоскости экватора точно под таким же углом, как ось Земли — 23,5°.
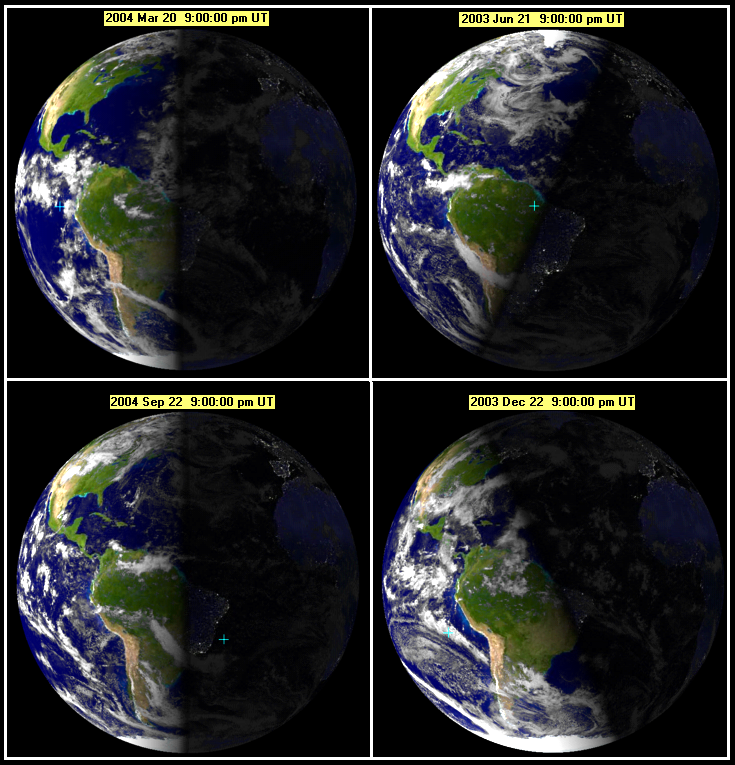
Равноденствие - момент пересечения небесного экватора центром видимого солнечного диска. Весеннее равноденствие наступает, когда Солнце переходит из южного полушария небесной сферы в северное и обычно происходит около 21 марта. Осеннее равноденствие бывает около 23 сентября. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце переходит из южного полушария небесной сферы в северное, т. е. пересекает небесный экватор "снизу вверх", наступает первый день весны, который называется днем весеннего равноденствия. Он приходится на 20–21 марта. В Южном полушарии Земли наступает астрономическая осень, а в Северном — астрономическая весна. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце достигает самой высокой (северной) точки на эклиптике, это день летнего солнцестояния. Приходится примерно на 21–22 июня. С этого дня в Северном полушарии начинается астрономическое лето, а в Южном — астрономическая зима.
Когда Солнце переходит из северного полушария небесной сферы в южное, т. е. пересекает небесный экватор "сверху вниз", это начало осени, день осеннего равноденствия. Обычно он приходится примерно на 23 сентября. В Южном полушарии Земли наступает астрономическая весна, а в Северном — астрономическая осень.
Когда Солнце достигает самой нижней (южной) точки на эклиптике, это день зимнего солнцестояния. Приходится примерно на 21–22 декабря. С этого дня в Северном полушарии начинается астрономическая зима, а в Южном — астрономическое лето.
- Информация о материале
- Просмотров: 21430
В астрономии, говоря о небесных телах, иногда используются специфические термины, характеризующие их цвет и яркость, например, звездная величина или показатель цвета.
Видимая звездная величина характеризует ту яркость, которую мы видим или можем увидеть. То есть, она определяет условия наблюдения объекта с Земли.
Эта величина берет начало со II века до р.Х., когда Гиппарх предложил делить все звезды по яркости на шесть величин - самые яркие и лучше всего видимые он назвал звездами первой величины, а самые тусклые - шестой.
Разумеется, такой субъективный подход для современных целей неприменим, к тому же, большая часть астрономических объектов невооруженным глазом не видна. При этом характеристика видимой яркости - вещь очень полезная. Поэтому в наше время классификация Гиппарха модернизирована и стала измеримой и объективной - и, несмотря на модернизацию, классы Гиппарха удалось сохранить.
Во-первых, яркость определяется числом квантов излучения объекта, принимаемых глазом или фотоприемником в единицу времени. Это позволяет оценить яркость объективно.
Во-вторых, она учитывает особенность человеческого зрения. Дело в том, что человек оценивает яркость не линейно, а логарифмически - психофизиологический закон Вебера-Фехнера утверждает, что для человека ощущение, вызванное неким раздражителем, изменяется пропорционально логарифму интенсивности раздражителя, то есть, применительно к свету, яркость света воспринимается нами пропорционально логарифму светового потока.
В связи с этим, видимая звездная величина m определяется по формуле:
где I - световой поток, а С - некая константа
Константа С выбирается так, чтобы шкала звездных величин была как можно ближе к гиппарховой, то есть, чтобы для весьма яркой звезды видимая величина m была равна нулю. Строго говоря, С выбирается так, чтобы в приведенной формуле m было равно нулю для объекта, создающего (без учета влияния земной атмосферы) освещенность 2,54·10-6 люкс.
Тогда звезда первой величины создает освещенность, примерно в 2,512 раз ниже указанной, второй величины - в 6,31 раз ниже и так далее. То есть, увеличение (уменьшение) звездной величины на единицу означает уменьшение (увеличение) силы света от источника примерно в 2,512 раза, а на пять единиц - ровно в сто раз. Объекты звездной величины более шести уже практически не видны невооруженным глазом.
m1 - m2 = 2.5 log (b2 / b1)
Мы можем также определить отношение, оперируя понятиями коэффициента яркости:
b2/b1 = 10x, where x = 0.4 (m1-m2)
При этом пока все еще не так просто. Звезда или иной объект излучает (или отражает) свет разных длин волн - а человек их воспринимает по-разному. При одной и той же интенсивности зеленый свет воспринимается ярче, красный - тусклее, а инфракрасный, разумеется, не воспринимается вовсе.
Абсолютные звёздные величины
Видимый блеск и видимая звёздная величина звезды зависят от её расстояния до наблюдателя – r. Чтобы освободиться от влияния расстояния, введено понятие об абсолютном блеске и абсолютной величине звезды.
Абсолютным блеском звезды L называется тот блеск, который она имела бы, будучи удалена от наблюдателя на расстояние равное 10 парсекам.
Так как освещённость убывает обратно пропорционально квадрату расстояния, то абсолютный блеск L и видимый блеск l связаны соотношением:
L/l = r2/100 = 2,512m-M
m – видимая звёздная величина, М – абсолютная звёздная величина, под которой понимают ту звёздную величину, которую бы имела звезда, будучи удалённой на расстояние, равное 10 парсекам.
Из указанного соотношения получаем формулу:
М = m + 5 - 5lg r
С учётом межзвёздного поглощения:
М = m + 5 - 5lg r - А(r)
где А(r) – поглощение света, пропорциональное расстоянию до звезды.
Эта формула позволяет вычислить абсолютную звёздную величину звезды, если известно расстояние, и вычислить расстояние, если известна абсолютная величина, по формуле:
lg r = (m - M)/5 + 1
Абсолютные звёздные величины могут быть болометрическими, визуальными, фотографическими.
Солнце имеет абсолютную звёздную величину +4,7m.
Часто используют светимость звезды – отношение абсолютного блеска звезды к абсолютному блеску Солнца.
Самые яркие звёзды ярче Солнца на 14m, они испускают больше энергии в 1 000 000 раз. Самые слабые слабее на 14m. Они испускают меньше энергии в 300 000 раз.
Отношение светимостей самых ярких и самых слабых звёзд достигает около 100 млрд.
Светимость (блеск) звезд
Представьте, что где-то в море в ночной тьме тихо мерцает огонек. Если бывалый моряк не объяснит вам, что это, вы часто и не узнаете: то ли перед вами фонарик на носу проходящей шлюпки, то ли мощный прожектор далекого маяка.
В том же положении в темную ночь находимся и мы, глядя на мерцающие звезды. Их видимый блеск зависит и от их истинной силы света, называемой светимостью (полное количествл энергии, излучаемой по всем направлениям), и от их расстояния до нас. Только знание расстояния до звезды позволяет подсчитать ее светимость по сравнению с Солнцем. Так например, светимость звезды, в десять раз менее яркой в действительности, чем Солнце, выразится числом 0,1.
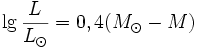
Истинную силу света звезды можно выразить еще иначе, вычислив, какой звездной величины она бы нам казалась, если бы она находилась от нас на стандартном расстоянии в 32,6 светового года, то есть на таком, что свет, несущийся со скоростью 300 000 км/сек, прошел бы его за это время.
где R - радиус звезды, Т - температура.
Принять такое стандартное расстояние оказалось удобным для различных расчетов. Яркость звезды, как и всякого источника света, изменяется обратно пропорционально квадрату расстояния от него. Этот закон позволяет вычислять абсолютные звездные величины или светимости звезд, зная расстояние до них.
Когда расстояния до звезд стали известны, то мы смогли вычислить их светимости, то есть смогли как бы выстроить их в одну шеренгу и сравнивать друг с другом в одинаковых условиях. Надо сознаться, что результаты оказались поразительными, поскольку раньше предполагали, что все звезды «похожи на наше Солнце». Светимости звезд оказались поразительно разнообразными, и их в нашей шеренге не сравнить ни с какой шеренгой пионеров.
Приведем только крайние примеры светимости в мире звезд.
Самой слабой из известных долго являлась звезда, которая в 50 тысяч раз слабее Солнца, и ее абсолютная величина светимости: +16,6. Однако, впоследствии были открыты и ещё более слабые звезды, светимость которых, по сравнению с солнцем, меньше в миллионы раз!

Размеры в космосе обманчивы: Денеб с Земли сияет ярче Антареса, а вот Пистолет — не виден совсем. Тем не менее, наблюдателю с нашей планеты и Денеб и Антарес кажутся просто незначительными точками, по сравнению с Солнцем. Насколько это неверно можно судить по простому факту: Пистолет выпускает в секунду столько же света, сколько Солнце — за год!
На другом краю шеренги звезд стоит «S» Золотой Рыбы, видимая только в странах Южного полушария Земли как звездочка восьмой величины (то есть даже не видимая без телескопа!). В действительности она в 400 тысяч раз ярче Солнца, и ее абсолютная величина светимости: —8,9.
Абсолютная величина светимости нашего Солнца равна +5. Не так уж и много! С расстояния в 32,6 светового года мы бы его плохо видели без бинокля.
Если яркость обычной свечи принять за яркость Солнца, то в сравнении с ней «S» Золотой Рыбы будет мощным прожектором, а самая слабая звезда слабее самого жалкого светлячка.
Итак, звезды — это далекие солнца, но их сила света может быть совершенно иной, чем у нашего светила. Образно выражаясь, менять наше Солнце на другое нужно было бы с оглядкой. От света одного мы ослепли бы, при свете другого бродили бы, как в сумерках.
- Информация о материале
- Просмотров: 45977
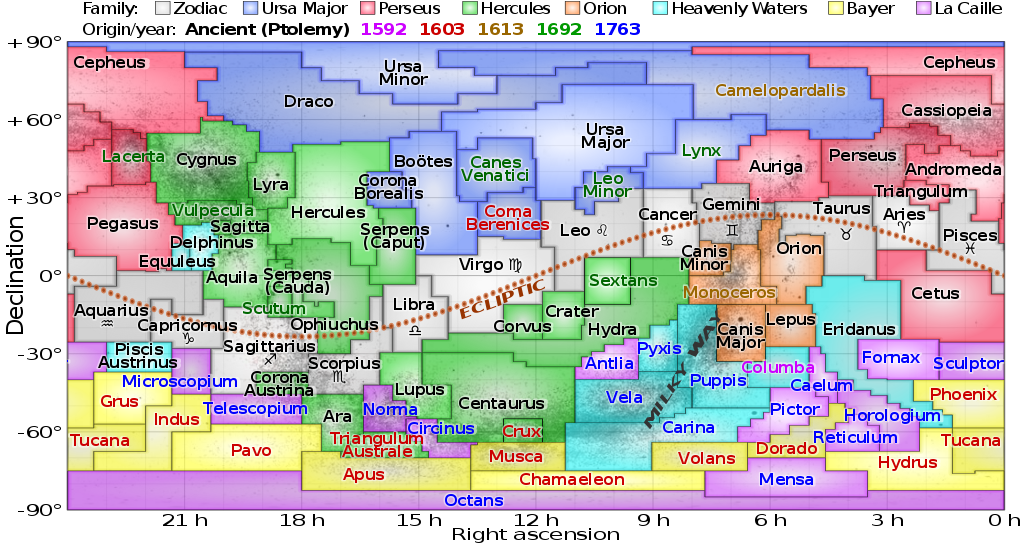
Созвездия — в современной астрономии участки, на которые разделена небесная сфера для удобства ориентирования на звёздном небе. В древности созвездиями назывались характерные фигуры, образуемые яркими звёздами.
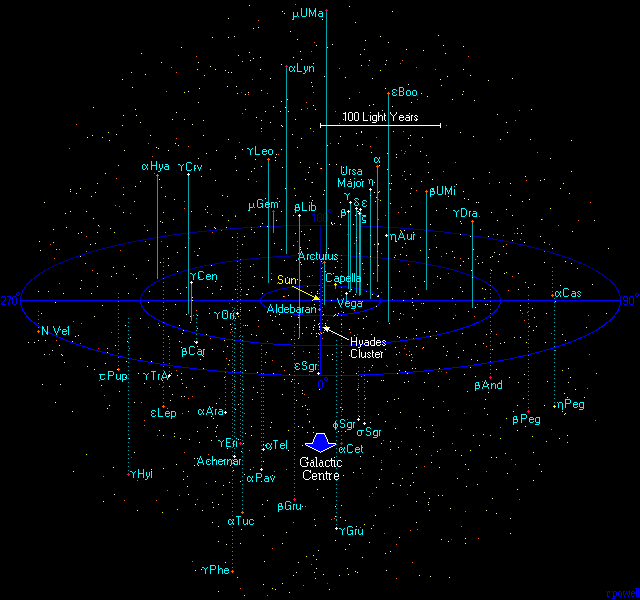
Звёзды, видимые на небесной сфере на небольших угловых расстояниях друг от друга, в трёхмерном пространстве могут быть расположены очень далеко друг от друга. Таким образом, в одном созвездии могут быть и очень близкие, и очень далёкие от Земли звёзды, никак друг с другом не связанные.
Но в древние времена люди видели во взаимном расположении звёзд некоторую систему и группировали их в соответствии с ней в созвездия. В течение истории наблюдатели выделяли различное число созвездий и их очертания, а происхождение названий некоторых древних созвездий так и не выяснено до конца. До XIX века под созвездиями понимались не области неба, а группы звёзд, которые нередко перекрывались. При этом получалось, что некоторые звёзды принадлежали сразу двум созвездиям, а некоторые бедные звёздами области не относились к какому-либо созвездию. В начале XIX века между созвездиями были проведены границы на небесной сфере, ликвидировавшие «пустоты» между созвездиями, однако их чёткого определения по-прежнему не было, и разные астрономы определяли их по-своему.
В 1922 году в Риме решением I Генеральной ассамблеи Международного астрономического союза был окончательно утверждён список из 88 созвездий, на которые было разбито звёздное небо, а в 1928 году были приняты чёткие и однозначные границы между этими созвездиями, проведённые строго по линиям постоянного прямого восхождения и линиям постоянного склонения в экваториальной системе небесных координат на эпоху 1875.0. В течение пяти лет в границы созвездий вносились уточнения. В 1935 году границы были окончательно утверждены, и астрономы договорились, что больше изменять их не будут. Следует, однако, помнить, что на звёздных картах, составленных для эпох, не совпадающих с эпохой 1875.0, в частности, всех современных картах, из-за прецессии земной оси границы созвездий сдвинулись и уже не совпадают с линиями постоянного прямого восхождения и склонения.
Из 88 созвездий только 48 являются древними, их названия и звёзды (но не изображения) были включены в каталог «Альмагест» Клавдия Птолемея, жившего во II веке н.э. Они охватывают область неба, доступную наблюдениям с юга Европы. Ранние изображения всех созвездий, введённых Птолемеем, можно найти в «Книге неподвижных звезд» ас-Суфи, жившего в 903—998 гг. Остальные современные созвездия были введены в XVII—XVIII веках в результате изучения южного неба (в эпоху великих географических открытий) и заполнения «пустых мест» на северном небе. Названия созвездий могут быть связаны с реальными или вымышленными животными (Большая Медведица, Лев, Дракон и т. д.), героями греческих мифов (Кассиопея, Андромеда, Персей и т. д.), а также с названиями предметов, очертания которых образуют яркие звёзды созвездий (Северная Корона, Треугольник, Весы, Южный Крест и др.).
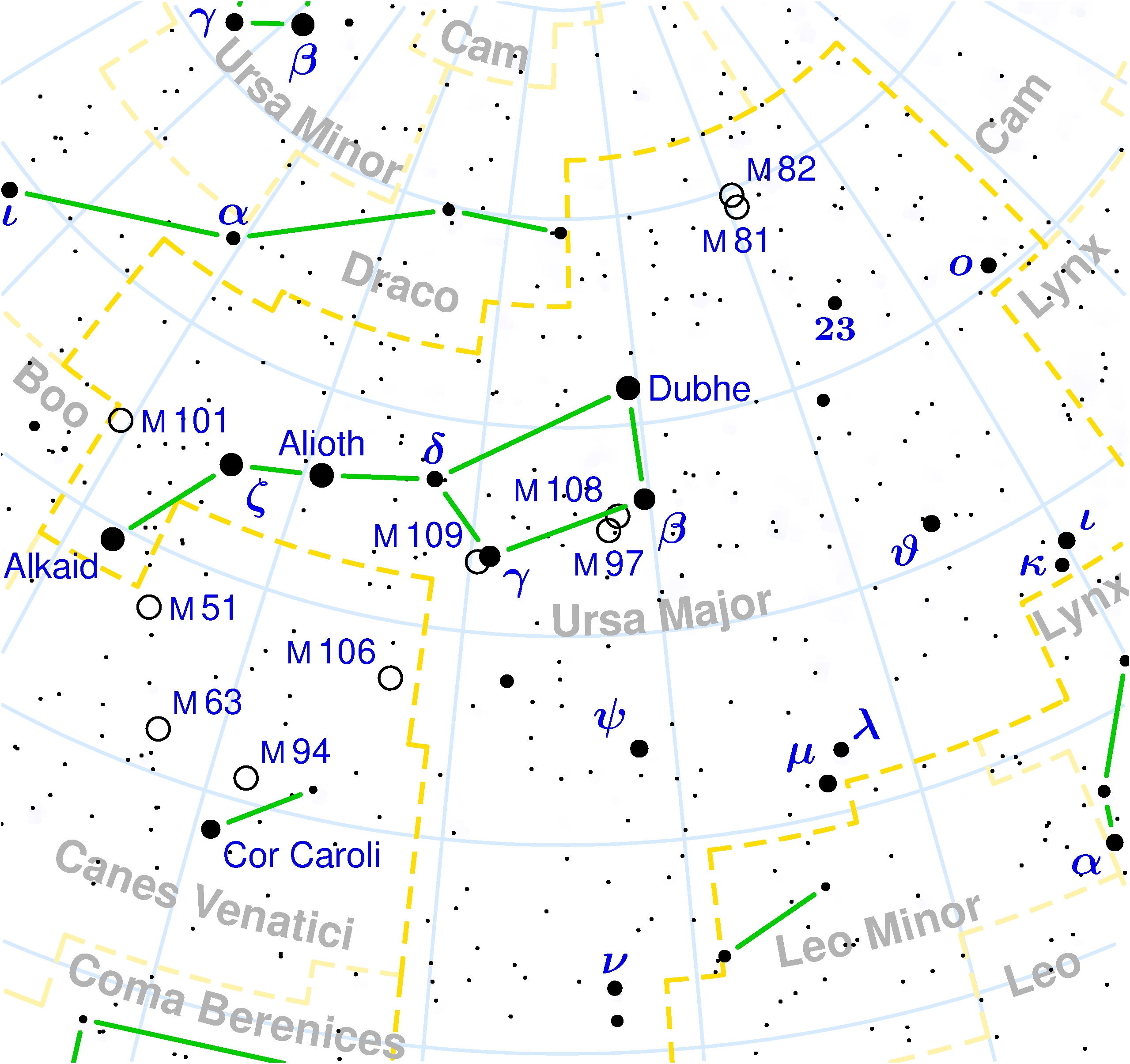
Значение деления неба на созвездия для наблюдательной астрономии заключается в том, что характерные контуры, состоящие из наиболее ярких звёзд, легко запомнить, что позволяет, зная, в каком созвездии находится объект, быстрее найти его.
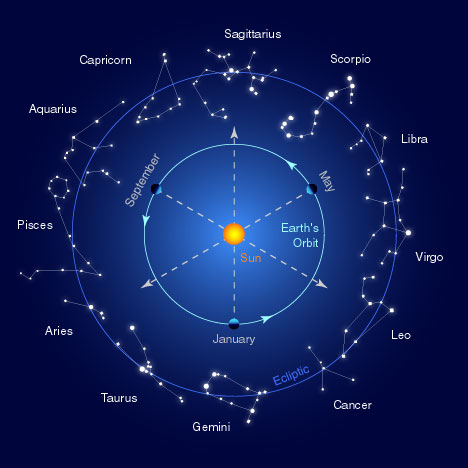
12 созвездий традиционно называют зодиакальными — такими, через которые проходит центр Солнца при годичном обороте по эклиптике. В период от 30 ноября до 17 декабря (эпоха 2014 г.) Солнце находится в созвездии Змееносца. Формально это созвездие тоже зодиакальное, но в астрологии его к зодиакальным не причисляют.
- Информация о материале
- Просмотров: 16678