Проведение лабораторной работы возможно, только если учащиеся освоили учебный материал по теме, знают порядок ее выполнения и соблюдают правила техники безопасности.
Содержание формы отчета (протокола)
1. Название и номер лабораторной работы.
2. Формулировка цели работы.
3. Краткое изложение теоретических основ работы.
4. Расчетные формулы.
5. Схема установки (в виде рисунка или электрической схемы). Все основные элементы схемы должны быть пронумерованы арабскими цифрами; расшифровка цифр должна быть дана в подписи под рисунком.
6. Таблица спецификации измерительных приборов.
7. Данные установки, табличные данные.
8. Таблицы результатов измерений.
9. Расчет искомых величин.
10. Расчет погрешностей прямых измерений.
11. Запись результатов прямых измерений в виде доверительных интервалов.
12. Расчет погрешностей косвенных измерений.
13. Запись окончательного результата в виде доверительного интервала.
14. Выводы по результатам экспериментов.
Погрешности физических измерений
Определение погрешностей в лабораторных работах
1. Погрешности физических измерений
Целью эксперимента является определение численного значения физической величины. Истинное значение физической величины – это такое значение, которое идеальным образом отображает соответствующие свойства объекта. Определение значения физической величины опытным путем с помощью специальных технических средств называется измерением.
1.1 Прямые и косвенные измерения
Прямым измерением называют измерение, при котором значение физической величины находят непосредственно из опытных данных, как показания использованных измерительных приборов. Косвенное измерение – такое, при котором значение физической величины находят на основании известной зависимости между этой величиной и другими величинами, определяемыми путем прямых измерений, то есть вычисляют по формуле.
Например, требуется определить ускорение тела при его прямолинейном равноускоренном движении без начальной скорости. Прямым измерением определяются время t (по секундомеру) и путь S (по линейке). Ускорение a определяется в результате косвенного измерения, то есть вычисляется по формуле a = 2S/t2, которая следует из соотношения S = at2/2.
При проведении измерений вследствие несовершенства методов и средств измерений, непостоянства внешних условий получают не истинное, а приближенное значение физической величины. Процесс измерения можно считать завершенным только тогда, когда указано не только значение измеренной величины, но и возможное отклонение его от истинного значения – погрешность.
1.2. Точность измерений. Погрешность измерений
1.2.1 Понятие погрешности
Точность измерений определяется близостью результата измерения к истинному значению измеряемой величины. Точность измерений характеризуется погрешностью измерения.
По форме числового выражения различают два вида погрешности: абсолютную и относительную.
Абсолютная погрешность Δx – величина возможного отклонения измеренного значения xизмер от истинного. Абсолютная погрешность выражается в единицах измеряемой величины и определяет границы числового интервала, в котором с вероятностью, близкой к единице, содержится истинное значение величины х (рис. 1).
Для истинного значения величины х справедливо соотношение:
xизмер – Δx ≤ x ≤ xизмер + Δx (1)
Числовой интервал 2Δх, в котором с вероятностью, близкой к единице, содержится истинное значение величины х, называется доверительным интервалом.

Рис. 1
Относительная погрешность εх – безразмерная величина, равная отношению абсолютной погрешности к измеренному значению величины, может быть выражена в процентах:
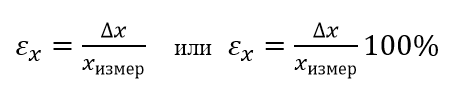
2. Определение погрешностей в лабораторных работах
2.1. Вычисление погрешностей прямых измерений
При оценке точности прямого измерения будем учитывать случайную погрешность и погрешность средства измерения.
2.1.1. Случайная погрешность
Выполнив n измерений величины x при неизменных условиях опыта, получим ее значения: x1, x2, x3, … xi ,… xn. Разброс значений xi связан со случайной погрешностью измерения величины x. Наилучшим приближением к истинному значению измеряемой величины x является среднее арифметическое измеренных значений:
![]()
Степень разброса результатов измерения и случайную погрешность можно оценить по величине среднего отклонения результатов от среднего значения:
![]()
где xi – (i-ое – любое, некоторое) значение измеренной величины; xср – среднее арифметическое значение, рассчитанное по формуле (3); n – количество измерений одной и той же величины в одних и тех же условиях.
2.1.2. Погрешность средств измерений (приборная, или инструментальная погрешность)
Погрешность средства измерения Δxпр – разность между показанием прибора и истинным значением измеряемой величины. Погрешность средства измерения является систематической, то есть даёт отклонение измеренной величины от истинного значения в одну сторону, но мы никогда не знаем, в какую именно. Любой прибор позволяет проводить измерения лишь с определенной точностью, погрешность зависит от вида прибора.
a) В приборах, у которых переход от одного значения к другому осуществляется скачком (стрелочный секундомер, весы с разновесами), инструментальная погрешность равна величине скачка.
b) Инструментальная погрешность приборов, снабженных нониусом (штангенциркуль, микрометр), равна точности нониуса:
![]()
c) Погрешности электроизмерительных стрелочных приборов рассчитываются по классу точности. Класс точности К определен отношением абсолютной погрешности Δх к используемому пределу измерения прибора Хmax и выражен в процентах
![]()
Следовательно, абсолютная погрешность измерения данным прибором рассчитывается по формуле:
![]()
Электроизмерительные приборы имеют восемь классов точности: К=(0.05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0). Чем выше класс точности, тем меньше значение К и меньше погрешность измерения.
d) Погрешность измерения цифровыми приборами рассчитывается по формулам, представленным в паспорте прибора.
e) Для прочих приборов с делениями (линейка, транспортир, термометр и т. п.) в качестве инструментальной погрешности принимается погрешность отсчёта, равная половине цены деления шкалы прибора.
2.1.3. Полная погрешность прямых измерений
Результирующая погрешность прямого измерения рассчитывается по формуле:
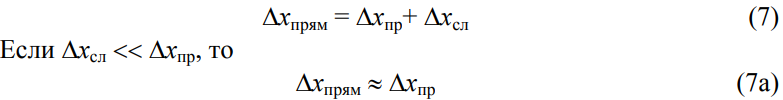
В случае, если Δхсл >> Δхпр, погрешностью средства измерений можно пренебречь. Однако, это одновременно говорит о том, что эксперимент проведен некачественно. Необходимо увеличить число измерений, чтобы уменьшить случайную погрешность. Если данная физическая величина измеряется один раз, то в качестве погрешности прямого измерения берут инструментальную погрешность Δхпр. Значение результата прямых измерений записывается в виде
x = xср ± Δx. (8)
2.2. Погрешности физических постоянных, табличных данных, данных установок (погрешности округления)
2.2.1. Физические постоянные (константы) считают точными величинами.
В этом случае значение данной величины подставляется в расчетную формулу с числом значащих цифр на одну больше, чем число значащих цифр, полученных в результате прямых измерений. При этом относительная погрешность округления константы окажется на порядок меньше погрешности прямого измерения, и ею можно пренебречь.
Многие табличные данные, используемые в расчетах, представлены с большой точностью. В этом случае при выборе числа значащих цифр для подстановки в расчетную формулу руководствуются предыдущим правилом.
2.2.2. Если же табличные данные, данные установок определены с точностью, сопоставимой с результатом прямых измерений, то такие данные считаются приближенными. В этом случае погрешность табличной величины принимают равной половине единицы младшего разряда используемого числа.
Пример1.
Пусть дано m = 8,5 г. Младший разряд числа – десятые (цифра 5). Абсолютная погрешность округления составляет половину от одной десятой:
![]()
Пример 2.
Пусть дано M = 4 г. Младший разряд числа – целые (цифра 4). Абсолютная погрешность округления составляет половину от одной целой:
![]()
2.3. Погрешность косвенных измерений
Результатом косвенных измерений является величина Y, рассчитанная по соответствующей формуле с использованием средних значений результатов прямых измерений. Погрешность косвенно измеряемой величины определяется погрешностями величин, полученных в процессе прямых измерений, а также погрешностями табличных данных и других постоянных, входящих в расчетную формулу.
Формула для вычисления относительной погрешности косвенного измерения
![]()
зависит от вида расчётной формулы для Y и приводится в описании каждой лабораторной работы. Абсолютная погрешность косвенного измерения ΔY очевидно может быть рассчитана по формуле:
ΔY = Y·εY
3. Оформление результатов работы
3.1. Правила записи чисел
В десятичной системе любое число записывают с помощью цифр 0, 1, 2, …, 9. Перечисленные цифры, кроме нуля, называют значащими. Нуль тоже относят к значащим цифрам, если он стоит в середине или в конце числа.
Например, все выделенные цифры в числе 00648,3600 являются значащими.
Результаты физических и технических экспериментов принято записывать только значащими цифрами. Наиболее удобна следующая запись: запятую ставят после первой отличной от нуля цифры, а значащую часть числа умножают на десять в соответствующей целой степени.
Например, вместо 0,000567 пишут 5,67 · 10-4, а вместо 3450000 пишут 3,45 · 106.
3.2. Округление результатов промежуточных расчетов
Количество значащих цифр в промежуточных расчётах не должно быть слишком большим. Как правило, числа, получаемые при работе с калькулятором, необходимо округлять, оставляя не более 4-5 значащих цифр.
Приведем примеры округления чисел до четырех значащих цифр:
0,0874425 ≈ 0,08744;
784,648 ≈ 784,6;
369279 ≈ 369300.
3.3. Правило округления абсолютной погрешности
Количество значащих цифр абсолютной погрешности не должно быть более двух.
Две цифры оставляют в том случае, если первая значащая цифра погрешности «1» или «2». Если первая цифра больше «2», то абсолютную погрешность округляют так, чтобы оставалась одна значащая цифра (см. далее примеры).
3.4. Правила округления и записи результата
Результат прямого или косвенного измерения (x или Y) должен быть округлен (или уточнен) с учетом погрешности измерения: разряд последней цифры результата должен совпадать с разрядом последней значащей цифры погрешности.
Результат записывается с указанием погрешности, определяющей доверительный интервал, с соответствующими единицами измерения:
Y = Y ± ΔY (10)
Пример 1.
В эксперименте было определено сопротивление проводника R = 2,756 Ом и абсолютная погрешность ΔR = 0,038 Ом.
По правилу 3.3 округляем абсолютную погрешность.
Первая значащая цифра «3», она больше «2» и стоит в разряде сотых. Следовательно, абсолютную погрешность округляем до одной значащей цифры, т.е. до разряда сотых, получаем ΔR = 0,04 Ом.
Далее применяем правило 3.4: в округленном значении абсолютной погрешности последняя значащая цифра «4» стоит в разряде сотых, следовательно, округляем результат до сотых: R = 2,76 Ом.
Окончательный результат записываем в виде: R = (2,76 ± 0,04) Ом.
Пример 2.
В эксперименте был определен коэффициент трения поверхности μ = 0,32438 и абсолютная погрешность Δμ = 0,0197.
По правилу 3.3 округляем абсолютную погрешность. Первая значащая цифра «1», следовательно, в абсолютной погрешности после округления должно быть две значащие цифры. Погрешность округляем до следующего разряда, т.е. до тысячных, получаем Δμ = 0,020.
Далее применяем правило 3.4: в округленном значении абсолютной погрешности последняя значащая цифра «0» стоит в разряде тысячных, следовательно, округляем результат до тысячных: μ = 0,324.
Окончательный результат записываем в виде: μ = 0,324 ± 0,020.
Пример 3.
В эксперименте была определена электроемкость конденсатора С = 4,1435 · 10-8 Ф и абсолютная погрешность ΔС = 1,23 · 10-9 Ф.
При записи результата представим значение величины и ее погрешность в виде X · 10-8, то есть с одинаковым показателем степени 10.
Окончательный результат получим в виде: С = (4,14 ± 0,12) · 10-8 Ф.
3.5. Правило сравнения результатов
Пусть истинное значение изучаемой величины известно или в процессе работы одна и та же величина определяется разными способами.
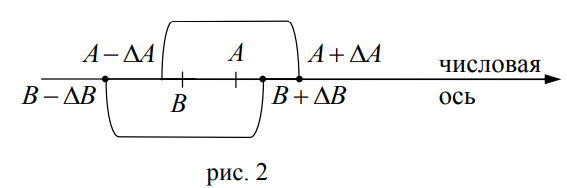
Значения двух величин А и В считаются совпадающими, если их доверительные интервалы перекрываются (рис. 2).
В этом случае, очевидно, выполняется соотношение:
|A – B| ≤ ΔA + ΔB (11)
3.6. Построение графиков
При изучении зависимости одной измеряемой величины от другой целесообразно представить результаты в форме графика. Главное достоинство графика – его наглядность. График позволяет получить общее качественное представление о характере зависимости, а также судить о соответствии экспериментальных данных той или иной теоретической зависимости. На графиках легко видеть “выпадение” точек, которые, как правило, соответствуют наблюдениям с грубыми погрешностями (промахами).
Графики следует строить на листах миллиметровой бумаги. Масштаб графика по обеим осям нужно выбирать так, чтобы предполагаемые зависимости обладали наибольшей наглядностью и заполняли большую часть графика.
Поле графика заключают в прямоугольную рамку, согласуя ее с основными линиями сетки. Стрелки на концах экспериментальных графиков не ставят (стрелки принято ставить лишь на иллюстрационных графиках качественного характера, построенных в произвольном масштабе).
На концах осей (если на оси используется лишь интервал, то и в начале оси) нужно указать обозначение соответствующих физических величин и единицы измерений этих величин. Учитывая, что миллиметровая бумага имеет очень мелкую сетку, оцифровывать нужно лишь деления крупной сетки. Допустимые значения, определяющие масштабы, следующие: 0,1,2,3,…; 0,2,4,6,…..; 0,5,10,…. Эти значения могут быть умножены на 10±n . Не следует наносить на оси числовые значения величин, полученных в ходе опыта!
Размеры экспериментальных точек должны быть соотнесены с погрешностями измерения соответствующих величин. Линия графика должна быть гладкой, она проводится так, чтобы по обе стороны от нее располагалось примерно одинаковое число “выпадающих” точек.
Под графиком должно быть подписано пояснение или название. Возможные варианты графического представления результатов показаны на рис. 3.
3.7. Нахождение физических величин по графику
Часто графики строятся с целью нахождения различных физических величин. Проще всего это сделать, если искомая физическая величина является коэффициентом пропорциональности в линейной функции y = k · x + y0 (например, жесткость пружины является коэффициентом пропорциональности между значениями силы упругости пружины и деформации).
Рекомендуемая последовательность действий:
1) нанести на график точки, соответствующие измеренным значениям;
2) провести оптимальную прямую через эти точки, таким образом, что бы количество экспериментальных точек, расположенных выше и ниже оптимальной прямой, было примерно равным (см. рис. 4);
3) ограничить полосу, в которой находятся точки, прямыми, параллельными оптимальной линии и проходящими через наиболее удаленные от оптимальной прямой точки (на рис. 4 – штриховые линии);
4) определить тангенс угла наклона оптимальной прямой по формуле
![]() в соответствующих единицах измерения.
в соответствующих единицах измерения.
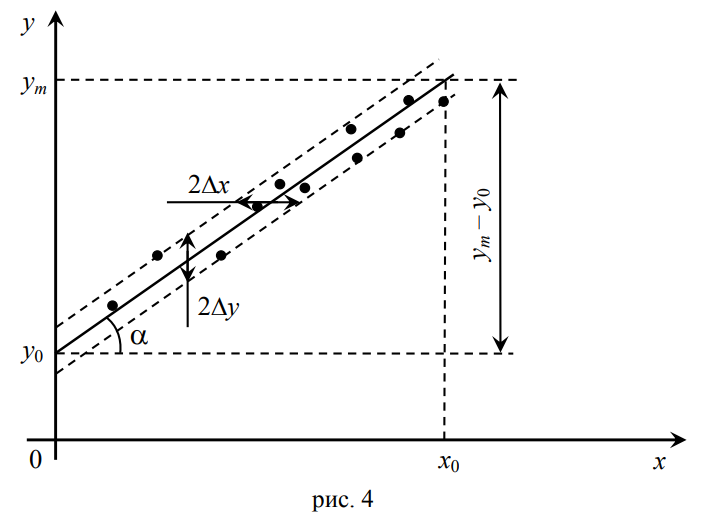
Погрешность искомой физической величины определяется по формулам
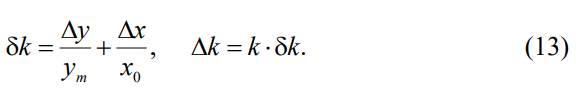
Абсолютные погрешности Δy и Δx определяются из графика, как показано на рис. 4, по соответствующим расстояниям между вспомогательными штриховыми линиями.
4. Пример обработки результатов измерений
Задание
Рассчитать объем краски, необходимый для окраски забора. Расход краски составляет P = 0,30 ± 0,04 л/м2 .
Размеры забора: высота h = 1,8 м, измерена однократно рулеткой с ценой деления 1 мм; длина измерена 5 раз дальномером с приборной погрешностью 0,2 м, результаты измерения представлены в таблице 1.
Таблица 1.
Результаты измерения длины забора дальномером
| № п/п | Li ,м |
| 1 | 15,8 |
| 2 | 16,2 |
| 3 | 16,0 |
| 4 | 15,8 |
| 5 | 15,8 |
Необходимый объем краски определяется по формуле V = S · P, где S – площадь поверхности забора.
Расчетная формула V = h · L · P.
Рассчитать погрешность, полученного объема краски по формулам относительная погрешность
εV = εh + εL + εP, (*)
абсолютная погрешность ΔV = V · εV.
Расчеты
Рассчитаем среднее значение результата прямого измерения длины забора
![]()
Площадь красочного покрытия
S = 1,8 · 15,92 = 28,66 м2.
Расчет результатов косвенных измерений
Необходимый объем краски V = 1,8 · 15,92 · 0,3 ≈ 8,597 л
Расчет погрешностей прямых измерений
– Погрешность высоты забора
Согласно п. 2.1.2 е) введения, приборная погрешность рулетки составляет Δhпр = 0,5 мм = 0,0005 м.
Поскольку величина h измерялась один раз, то, согласно п. 2.1.3 введения, полная погрешность высоты забора принимается равной ее приборной погрешности Δh = Δhпр = 0,0005 м.
Рассчитаем относительную погрешность высоты забора
![]()
– Погрешность длины забора
После многократных измерений необходимо оценить случайную погрешность. Для этого найдем отклонения от среднего ΔLi и запишем их в соответствующие ячейки таблицы 2.
Таблица 2. Расчет случайной погрешности измерения длины забора
| № п/п | Li ,м | |Lср - Li|, м |
| 1 | 15,8 | 0,12 |
| 2 | 16,2 | 0,28 |
| 3 | 16,0 | 0,08 |
| 4 | 15,8 | 0,12 |
| 5 | 15,8 | 0,12 |
| средн. | 15,92 | 0,144 |
Вычислим случайную погрешность длины забора
![]()
Вычислим полную погрешность длины забора ΔL = 0,2 + 0,144 = 0,344 ≈ 0,3 м. (округлили до одной значащей цифры)
Вычислим относительную погрешность длины забора
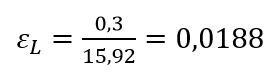
Запишем результат измерения длины забора в виде доверительного интервала
L = (15,9 ± 0,3) м
Рассчитаем относительную погрешность расхода краски
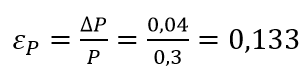
Расчет погрешностей косвенных измерений
По (*) ΔV = 2,78 · 10-4 + 0,0188 + 0,133 ≈ 0,152 ≈ 15 %, ΔV = 0,152 · 8,597 = 1,3067 ≈ 1,3 л. (округлили до двух значащих цифр)
Запишем найденное значение объема краски в виде доверительного интервала
Ответ: V = (8,6 ± 1,3) л.
Левая граница доверительного интервала для объема краски оказалась равной 8,6 - 1,3 = 7,3 л, правая граница – 8,6 + 1,3 = 9,9 л.
Изобразим на числовой оси в выбранном масштабе значение необходимого объема краски с доверительным интервалом.
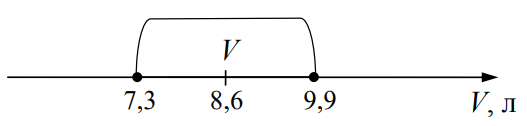
Выводы
Оценка погрешности позволяет определить, сколько краски нужно взять, что бы не оказаться перед недокрашенным забором – ведь при всех измерениях были допущены погрешности. На основании выполненных расчетов нельзя сказать, сколько потребуется краски точно, можно утверждать, что будет израсходовано не менее 7,3 литров краски и не более 9,9 литров.
Создано по материалам источника.
