В астрономии, говоря о небесных телах, иногда используются специфические термины, характеризующие их цвет и яркость, например, звездная величина или показатель цвета.
Видимая звездная величина характеризует ту яркость, которую мы видим или можем увидеть. То есть, она определяет условия наблюдения объекта с Земли.
Эта величина берет начало со II века до р.Х., когда Гиппарх предложил делить все звезды по яркости на шесть величин - самые яркие и лучше всего видимые он назвал звездами первой величины, а самые тусклые - шестой.
Разумеется, такой субъективный подход для современных целей неприменим, к тому же, большая часть астрономических объектов невооруженным глазом не видна. При этом характеристика видимой яркости - вещь очень полезная. Поэтому в наше время классификация Гиппарха модернизирована и стала измеримой и объективной - и, несмотря на модернизацию, классы Гиппарха удалось сохранить.
Во-первых, яркость определяется числом квантов излучения объекта, принимаемых глазом или фотоприемником в единицу времени. Это позволяет оценить яркость объективно.
Во-вторых, она учитывает особенность человеческого зрения. Дело в том, что человек оценивает яркость не линейно, а логарифмически - психофизиологический закон Вебера-Фехнера утверждает, что для человека ощущение, вызванное неким раздражителем, изменяется пропорционально логарифму интенсивности раздражителя, то есть, применительно к свету, яркость света воспринимается нами пропорционально логарифму светового потока.
В связи с этим, видимая звездная величина m определяется по формуле:
где I - световой поток, а С - некая константа
Константа С выбирается так, чтобы шкала звездных величин была как можно ближе к гиппарховой, то есть, чтобы для весьма яркой звезды видимая величина m была равна нулю. Строго говоря, С выбирается так, чтобы в приведенной формуле m было равно нулю для объекта, создающего (без учета влияния земной атмосферы) освещенность 2,54·10-6 люкс.
Тогда звезда первой величины создает освещенность, примерно в 2,512 раз ниже указанной, второй величины - в 6,31 раз ниже и так далее. То есть, увеличение (уменьшение) звездной величины на единицу означает уменьшение (увеличение) силы света от источника примерно в 2,512 раза, а на пять единиц - ровно в сто раз. Объекты звездной величины более шести уже практически не видны невооруженным глазом.
m1 - m2 = 2.5 log (b2 / b1)
Мы можем также определить отношение, оперируя понятиями коэффициента яркости:
b2/b1 = 10x, where x = 0.4 (m1-m2)
При этом пока все еще не так просто. Звезда или иной объект излучает (или отражает) свет разных длин волн - а человек их воспринимает по-разному. При одной и той же интенсивности зеленый свет воспринимается ярче, красный - тусклее, а инфракрасный, разумеется, не воспринимается вовсе.
Абсолютные звёздные величины
Видимый блеск и видимая звёздная величина звезды зависят от её расстояния до наблюдателя – r. Чтобы освободиться от влияния расстояния, введено понятие об абсолютном блеске и абсолютной величине звезды.
Абсолютным блеском звезды L называется тот блеск, который она имела бы, будучи удалена от наблюдателя на расстояние равное 10 парсекам.
Так как освещённость убывает обратно пропорционально квадрату расстояния, то абсолютный блеск L и видимый блеск l связаны соотношением:
L/l = r2/100 = 2,512m-M
m – видимая звёздная величина, М – абсолютная звёздная величина, под которой понимают ту звёздную величину, которую бы имела звезда, будучи удалённой на расстояние, равное 10 парсекам.
Из указанного соотношения получаем формулу:
М = m + 5 - 5lg r
С учётом межзвёздного поглощения:
М = m + 5 - 5lg r - А(r)
где А(r) – поглощение света, пропорциональное расстоянию до звезды.
Эта формула позволяет вычислить абсолютную звёздную величину звезды, если известно расстояние, и вычислить расстояние, если известна абсолютная величина, по формуле:
lg r = (m - M)/5 + 1
Абсолютные звёздные величины могут быть болометрическими, визуальными, фотографическими.
Солнце имеет абсолютную звёздную величину +4,7m.
Часто используют светимость звезды – отношение абсолютного блеска звезды к абсолютному блеску Солнца.
Самые яркие звёзды ярче Солнца на 14m, они испускают больше энергии в 1 000 000 раз. Самые слабые слабее на 14m. Они испускают меньше энергии в 300 000 раз.
Отношение светимостей самых ярких и самых слабых звёзд достигает около 100 млрд.
Светимость (блеск) звезд
Представьте, что где-то в море в ночной тьме тихо мерцает огонек. Если бывалый моряк не объяснит вам, что это, вы часто и не узнаете: то ли перед вами фонарик на носу проходящей шлюпки, то ли мощный прожектор далекого маяка.
В том же положении в темную ночь находимся и мы, глядя на мерцающие звезды. Их видимый блеск зависит и от их истинной силы света, называемой светимостью (полное количествл энергии, излучаемой по всем направлениям), и от их расстояния до нас. Только знание расстояния до звезды позволяет подсчитать ее светимость по сравнению с Солнцем. Так например, светимость звезды, в десять раз менее яркой в действительности, чем Солнце, выразится числом 0,1.
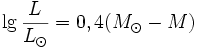
Истинную силу света звезды можно выразить еще иначе, вычислив, какой звездной величины она бы нам казалась, если бы она находилась от нас на стандартном расстоянии в 32,6 светового года, то есть на таком, что свет, несущийся со скоростью 300 000 км/сек, прошел бы его за это время.
где R - радиус звезды, Т - температура.
Принять такое стандартное расстояние оказалось удобным для различных расчетов. Яркость звезды, как и всякого источника света, изменяется обратно пропорционально квадрату расстояния от него. Этот закон позволяет вычислять абсолютные звездные величины или светимости звезд, зная расстояние до них.
Когда расстояния до звезд стали известны, то мы смогли вычислить их светимости, то есть смогли как бы выстроить их в одну шеренгу и сравнивать друг с другом в одинаковых условиях. Надо сознаться, что результаты оказались поразительными, поскольку раньше предполагали, что все звезды «похожи на наше Солнце». Светимости звезд оказались поразительно разнообразными, и их в нашей шеренге не сравнить ни с какой шеренгой пионеров.
Приведем только крайние примеры светимости в мире звезд.
Самой слабой из известных долго являлась звезда, которая в 50 тысяч раз слабее Солнца, и ее абсолютная величина светимости: +16,6. Однако, впоследствии были открыты и ещё более слабые звезды, светимость которых, по сравнению с солнцем, меньше в миллионы раз!

Размеры в космосе обманчивы: Денеб с Земли сияет ярче Антареса, а вот Пистолет — не виден совсем. Тем не менее, наблюдателю с нашей планеты и Денеб и Антарес кажутся просто незначительными точками, по сравнению с Солнцем. Насколько это неверно можно судить по простому факту: Пистолет выпускает в секунду столько же света, сколько Солнце — за год!
На другом краю шеренги звезд стоит «S» Золотой Рыбы, видимая только в странах Южного полушария Земли как звездочка восьмой величины (то есть даже не видимая без телескопа!). В действительности она в 400 тысяч раз ярче Солнца, и ее абсолютная величина светимости: —8,9.
Абсолютная величина светимости нашего Солнца равна +5. Не так уж и много! С расстояния в 32,6 светового года мы бы его плохо видели без бинокля.
Если яркость обычной свечи принять за яркость Солнца, то в сравнении с ней «S» Золотой Рыбы будет мощным прожектором, а самая слабая звезда слабее самого жалкого светлячка.
Итак, звезды — это далекие солнца, но их сила света может быть совершенно иной, чем у нашего светила. Образно выражаясь, менять наше Солнце на другое нужно было бы с оглядкой. От света одного мы ослепли бы, при свете другого бродили бы, как в сумерках.





