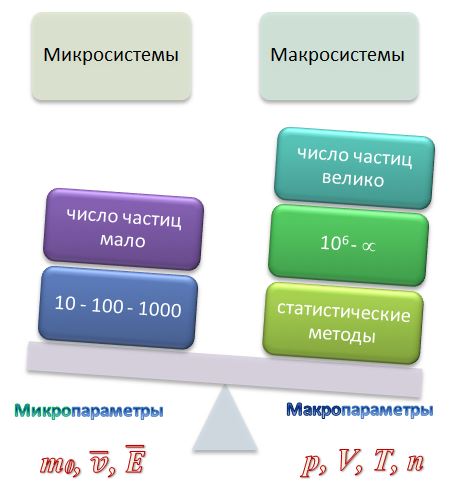
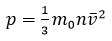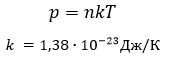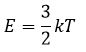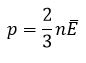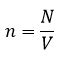Задача МКТ - установить связь между микро и макропараметрами газов.
Идеальный газ представляет собой простейшую модель газа, в которой пренебрегают энергией взаимодействия между отдельными частицами. Действительно, если газ достаточно разрежен, столкновения между его частицами происходят редко, в то время как скорости их велики, поэтому кинетическая энергия частиц значительно больше потенциальной энергии их взаимодействия.
Идеализация:
- объем молекулы равен нулю (материальная точка);
- столкновения между молекулами абсолютно упруги;
- силы притяжения между молекулами пренебрежимо малы.
Макроскопические параметры – величины, характеризующие состояние термодинамической системы без учета молекулярного строения тел
Давление p, объем V, температура T
Давление в МКТ образуется из-за ударов молекул о стенки сосуда при тепловом движении.

Идеальный газ – модель газа, в которой молекулы считают материальными точками и не учитывают силы взаимодействия между ними.
Среднее значение квадрата скорости молекул
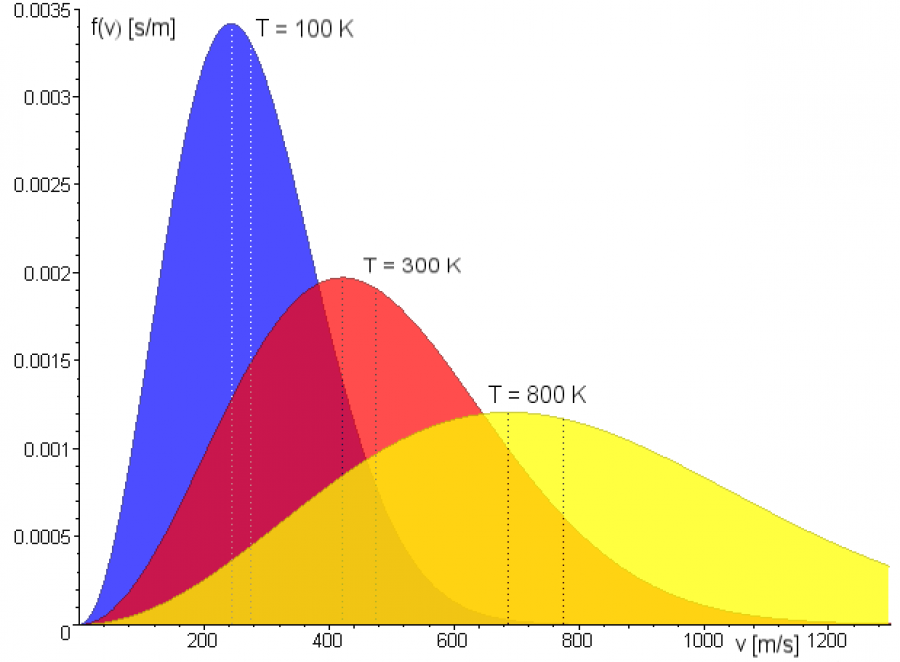
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Дж. Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля.
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость υкв = √v2.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются.
Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа.
Основное уравнение МКТ для идеального газа
Основное уравнение МКТ связывает макроскопические параметры состояния газа с характеристиками движения его молекул. Давление газа на стенки сосуда есть следствие столкновений молекул газа со стенками. Средняя сила, возникающая от совокупного действия всех молекул газа, определяет давление газа.
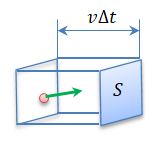
Представим себе сосуд в виде прямоугольного параллелепипеда, в котором содержится идеальный газ. Вычислим давление газа на одну из стенок сосуда площадью S.
Рассмотрим удар одной молекулы, которая до удара двигалась к стенке. Согласно закону сохранения импульса она передает стенке импульс 2m0vx.
За время Δt площадки S достигнут только те молекулы, которые заключены в объеме параллелепипеда с основанием S и высотой vΔt. Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трёх взаимно перпендикулярных направлений, так что вдоль каждого из них движется 1/3 молекул, причем половина молекул (1/6) движется вдоль данного направления в одну сторону, половина - в противоположную:
N = 1/6 nV = 1/6 nSvΔt.
За время Δt полное изменение импульса составит Δp = Np0 = 1/6 nSvΔt 2 m0 v = 1/3 nSm0 v2
Сила, с которой молекулы воздействуют на стенку, F = Δp/ Δt
а давление, обусловленное этой силой, т.е. давление газа, равно p = F/S
Зависимость давления от концентрации и температуры
- постоянная Больцмана
Средняя кинетическая энергия молекул
Концентрация
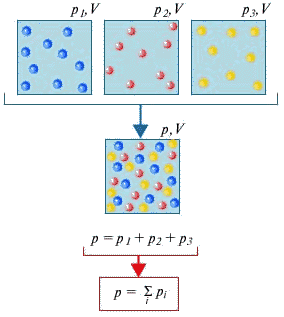
Закон Дальтона
В 1801 г. Джон Дальтон установил, что давление смеси нескольких газов равно сумме парциальных давлений всех газов, составляющих смесь. Этот закон получил название закона парциальных давлений газов. Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.
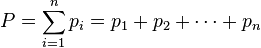
Воздух в комнате, где мы находимся, представляет собой смесь нескольких газов, в основном — азота (около 80%) и кислорода (около 20%). Парциальное давление каждого из этих газов — это давление, которое имел бы газ, если бы он один занимал весь объем. К примеру, если бы все газы, кроме азота, удалили из комнаты, то давление того, что осталось, и было бы парциальным давлением азота. Закон Дальтона утверждает, что общее давление всех газов вместе взятых равно сумме парциальных давлений каждого газа в отдельности.