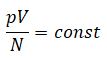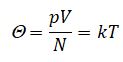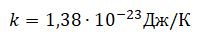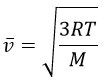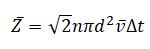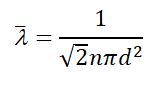Температура характеризует состояние теплового равновесия термодинамической системы. Все тела, находящиеся друг с другом в состоянии теплового равновесия, имеют одну и ту же температуру.
Температура – степень нагретости тела. Измерение температуры термометрами основано на изменении какого-либо физического параметра при нагревании, например, расширении тел при нагревании или изменении электрического сопротивления.
Все тела при нагревании расширяются, это свойство можно использовать при создании термометров, термометрическим веществом которых является не только жидкость, но и газ, и твердое тело.
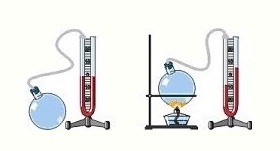
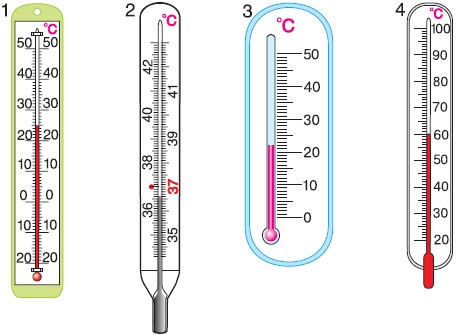

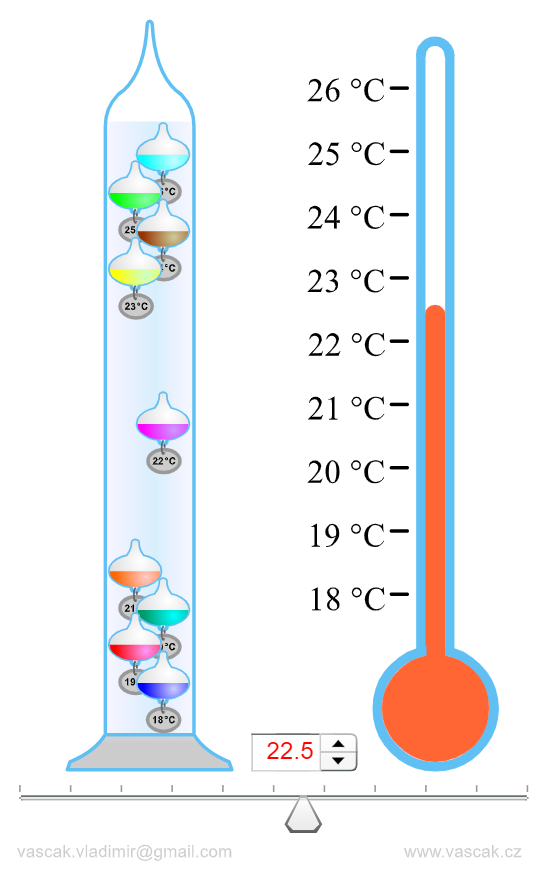
Термометр Галилея
Поплавки по-разному наполнены жидкостью таким образом, что их средняя плотность различна: самая маленькая плотность у верхнего, самая большая — у нижнего, но у всех близка к плотности воды, отличаясь от неё незначительно. С понижением температуры воздуха в помещении соответственно понижается температура воды в сосуде, вода сжимается, и плотность её становится больше.
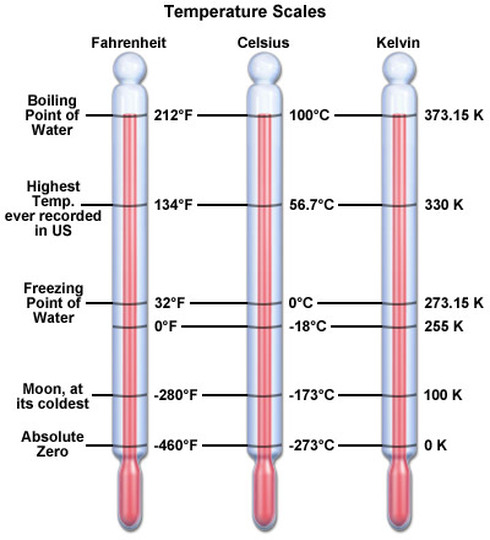
Шкалы температур
|
Шкала Реомюра Предложена в 1730 году Р. А. Реомюром, который описал изобретённый им спиртовой термометр. Единица — градус Реомюра (°R), 1 °R равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °R) и кипения воды (80 °R) 1 °R = 1,25 °C. Шкала Фаренгейта В этой шкале на 100 градусов раздёлен интервал от температуры самой холодной зимы в городе, где жил Фаренгейт в Голландии, до температуры человеческого тела. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F - 32), 1 °F = 5/9 °С. Предложена Г. Фаренгейтом в 1724. Шкала Цельсия В быту используется шкала Цельсия, в которой за 0 принимают точку замерзания воды, а за 100° точку кипения воды при атмосферном давлении. Поскольку температура замерзания и кипения воды недостаточно хорошо определена, в настоящее время шкалу Цельсия определяют через шкалу Кельвина: градус Цельсия равен кельвину, абсолютный ноль принимается за −273,15 °C. Шкала Кельвина В термодинамике используется шкала Кельвина, в которой температура отсчитывается от абсолютного нуля (состояние, соответствующее минимальной теоретически возможной внутренней энергии тела), а один кельвин равен 1/273.16 расстояния от абсолютного нуля до тройной точки воды (0,01 °С, состояния, при котором лёд, вода и водяной пар находятся в равновесии). T = t0C + 273 |
|
Температура характеризует скорость движения молекул, а значит, и создаваемое ими давление. При понижении температуры скорость теплового движения молекул уменьшается. Существует такое значение температуры, при котором всякое тепловое движение прекращается. Эта температура называется абсолютный ноль или точка нулевого давления.
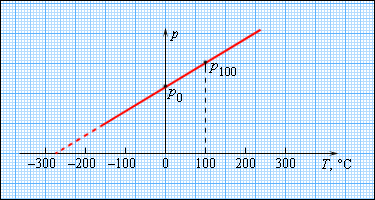
Тепловое равновесие – состояние термодинамической системы, при котором все макроскопические параметры сколь угодно долго остаются неизменными.
Температура является мерой кинетической энергии хаотического движения молекул в макроскопических телах.
Энергетическая температура
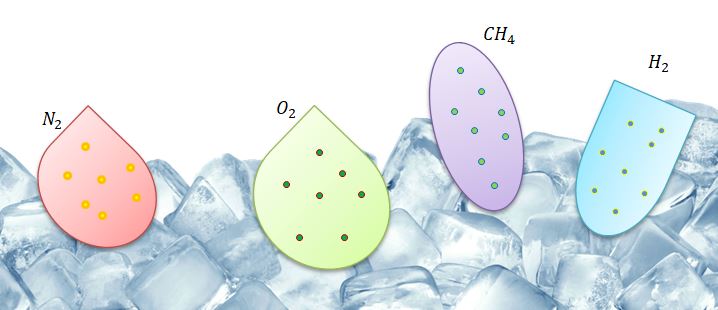
Если провести опыт, положив несколько сосудов с разными газами в лед, то можно заметить, что хотя разные характеристики каждого газа, но их отношение одинаково:
Поскольку данное соотношение зависит только от температуры и имеет размерность энергии, его называют энергетической температурой:
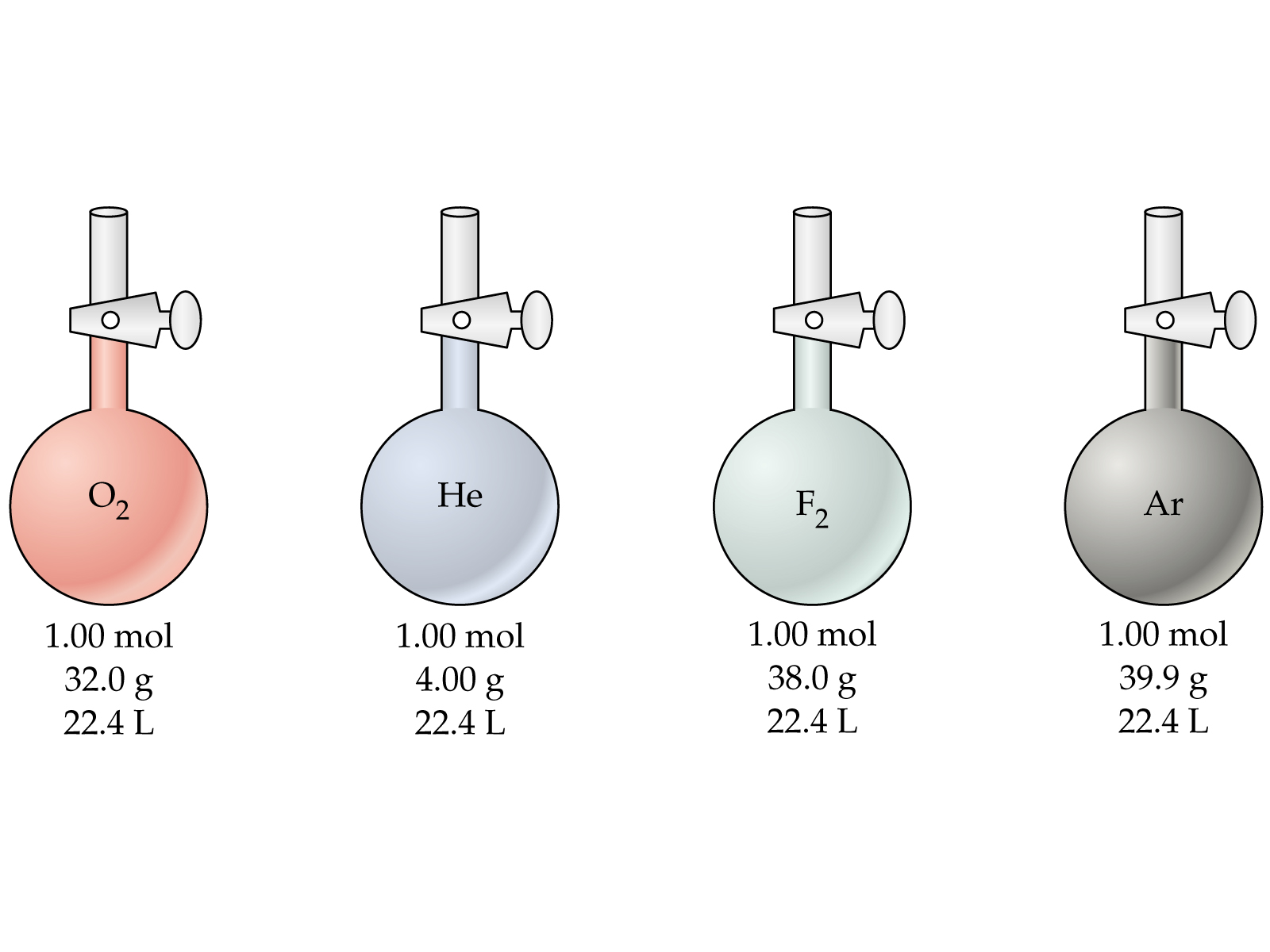
k - коэффициент пропорциональности между энергетической и абсолютной температурой, постоянная Больцмана
Закон Авогадро следует из определения энергетической температуры: В равных объемах любых газов, взятых при одной и той же температуре и при одинаковом давлении, содержится одно и то же число молекул.
Из закона Авогадро вытекает важное следствие: моль любого газа при нормальных условиях (0ºС (273 К) и давлении 101,3 кПа) занимает объем, равный 22,4 л. В этом объеме содержится 6,02·1023 молекул газа (число Авогадро).
Опыт Штерна по определению скоростей теплового движения атомов, проведённый немецким физиком Отто Штерном в 1920 году. Опыт являлся одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.
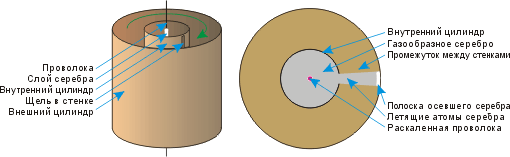
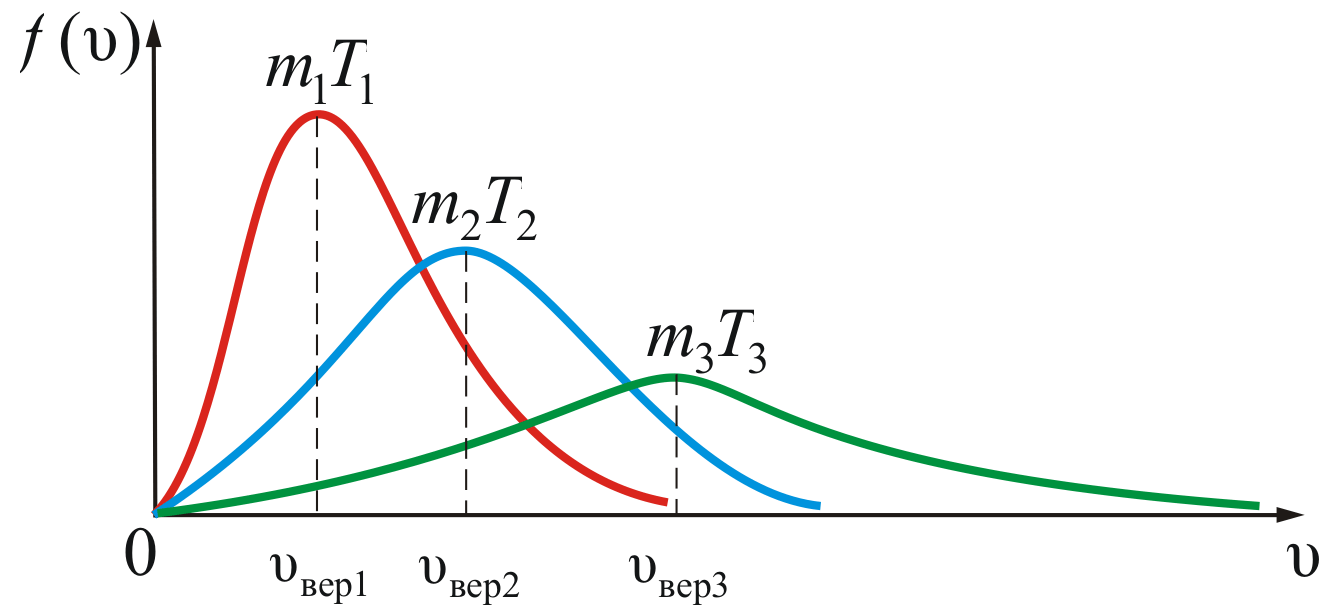
Среднеквадратичная скорость теплового движения атомов (молекул)
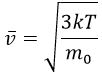
Средняя длина свободного пробега молекул
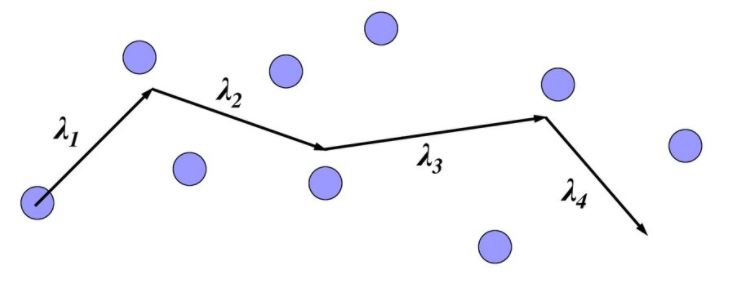
Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Между двумя последовательными соударениями молекулы, двигаясь равномерно и прямолинейно, проходят некоторые расстояния, называемые длинами свободных пробегов λ. Эти расстояния могут быть самыми разными, то есть λ - случайная величина. Поэтому вводят понятие средней длины свободного пробега <λ>, под которой понимают среднее расстояние, проходимое молекулой между двумя последовательными столкновениями со средней арифметической скоростью <v>.
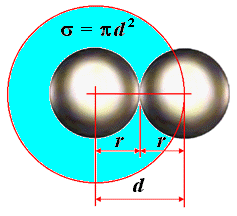
Будем считать, что молекулы газа представляют собой шарики диаметром d. Минимальное расстояние, на которое могут сблизиться при столкновении центры двух молекул, также равно d. Это расстояние называется эффективным диаметром молекулы. Круг радиусом d с центром в центре рассматриваемой молекулы площадью πd2 называется эффективным сечением молекулы.
Если молекула за некоторый промежуток времени Δt претерпевает в среднем <Z> столкновений, то средняя длина ее свободного пробега равна
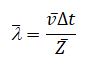
Предположим для простоты, что движется только одна рассматриваемая молекула, а остальные неподвижны. Кроме того, ломаную траекторию молекулы мысленно спрямим и будем считать движение молекул условно прямолинейным. Тогда за время Δt эта молекула претерпит <Z> столкновений, равное числу молекул, центры которых лежат в прямом цилиндре с основанием, равным эффективному сечению молекулы, и высотой, равной пути, проходимому молекулой за это время, то есть <v>Δt:
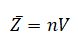
где n - концентрация молекул, V - объем цилиндра.
Тогда получим
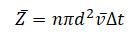
При учете движения всех молекул среднее число столкновений, испытываемых одной молекулой за некоторый промежуток времени Δt, равно
Получим выражение для средней длины свободного пробега молекулы: