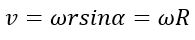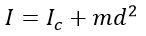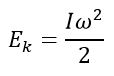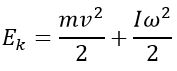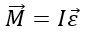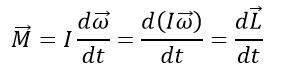Вращательным движением твердого тела называется такое движение, при котором все точки тела движутся по концентрическим окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Движение тела как целого можно характеризовать только такими величинами, которые в данный момент времени для всех его точек одинаковы. Поэтому вращательное движение твердого тела характеризуют не линейными, а угловыми величинами: углом поворота Δφ, угловой скоростью ω и угловым ускорением ε.

Угловой скоростью вращения твердого тела называется вектор ω, численно равный первой производной от угла поворота по времени

 или ,

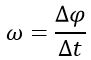
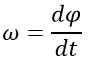
и направленный вдоль оси вращения таким образом, чтобы из его конца вращение было видно происходящим против часовой стрелки. Также направление вектора угловой скорости можно определить по правилу буравчика.

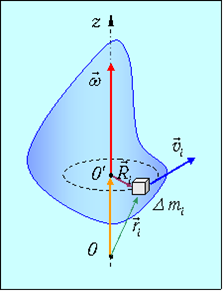
Линейная скорость v произвольной точки М вращающегося тела определяется по формуле Эйлера

,

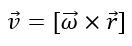
где r - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Модуль вектора линейной скорости пропорционален расстоянию до оси вращения:

Угловым ускорением вращения твердого тела называется вектор ε, численно равный модулю второй производной от угла поворота по времени или первой производной от угловой скорости по времени

,

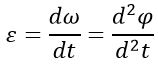
и направленный в ту же сторону, что и вектор угловой скорости, если движение ускоренной и в противоположную сторону от вектора угловой скорости, если движение замедленное. Если тело вращается равномерно, то ε = 0.

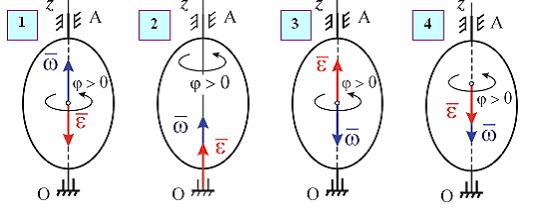
Вектор ускорения каждой точки тела, вращающегося вокруг неподвижной оси, можно разбить на две составляющие: нормальное (центростремительное) и тангенциальное. Вектор нормального ускорения направлен к оси вращения, а по модулю определяется по формуле 

.

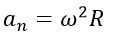
Вектор тангенциального ускорения направлен по касательной к окружности, а по модулю определяется по формуле

.

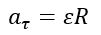
Отсюда модуль полного ускорения определяется по формуле

.

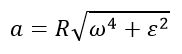
Разобьем вращающееся тело на малые элементы Δm_i. Расстояния до оси вращения обозначим через R_i, модули линейных скоростей – через v_i. Тогда кинетическую энергию вращающегося тела можно записать в виде:

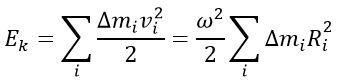
Физическая величина, зависящая от распределения масс вращающегося тела относительно оси вращения, называется моментом инерции тела относительно данной оси. Это величина, характеризующая инертность тела при вращательном движении.

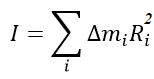
Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг∙м²).

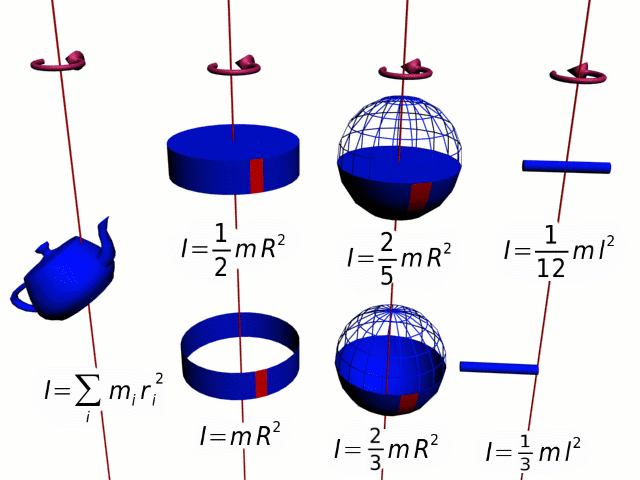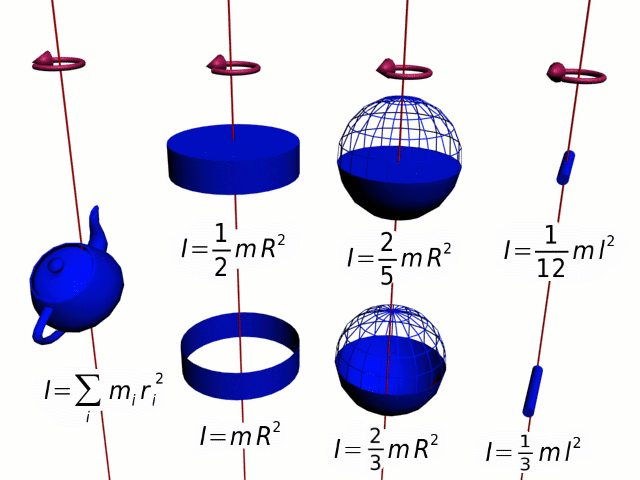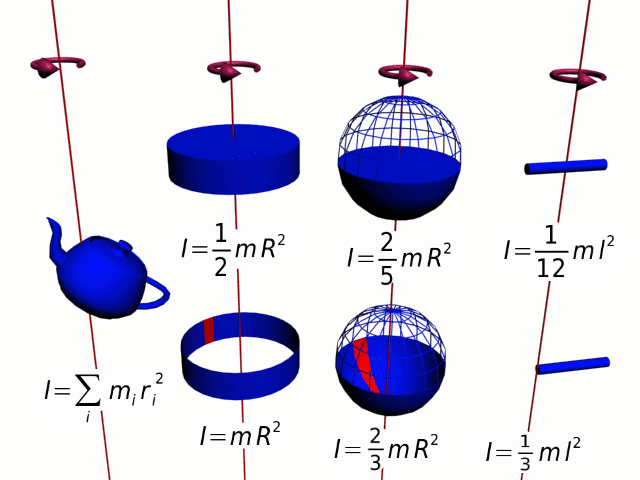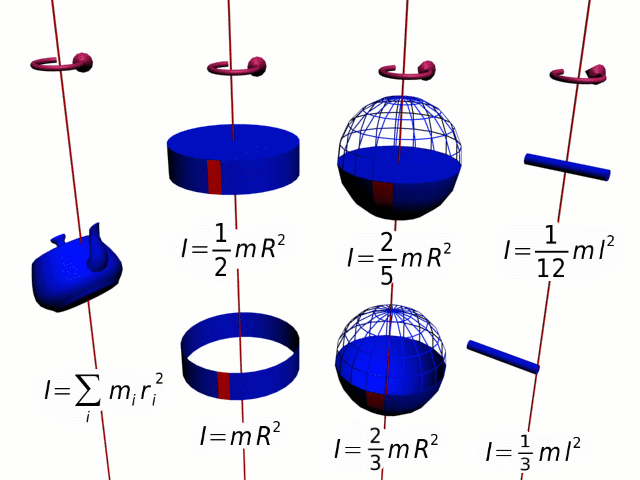
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции I_C этого тела относительно оси, проходящей через центр масс тела и параллельной первой. Теорема Штейнера:

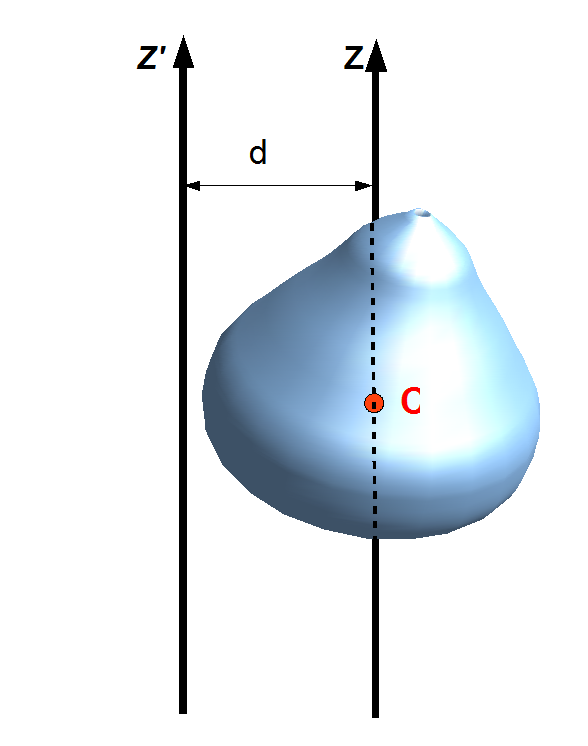
Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде

Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности. При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка. Такое движение называется плоским.

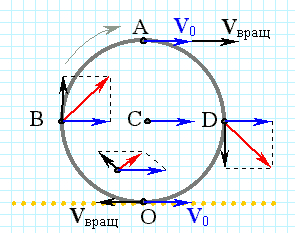
При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:

Для описания вращательного движения вводятся величины, аналогичные тем, которыми характеризуют поступательное движение: момент силы аналогичен силе, момент инерции аналогичен массе.

Основной закон динамики вращательного движения (II закон Ньютона для вращательного движения) имеет вид:

где M – результирующий момент сил, действующий на тело, I – момент инерции тела, ε – угловое ускорение, полученное телом.

где L = Iω – момент импульса, или кинетический момент, твердого тела. Эта величина аналогична импульсу точки p = mv.

Закон сохранения момента импульса:

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется (момент импульса замкнутой системы остается неизменным): 

L = const

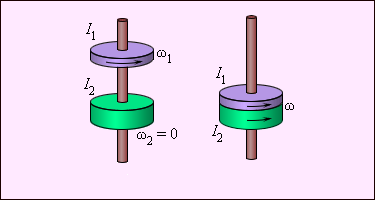
Пример: Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I₁ω₁ = (I₁ + I₂)ω

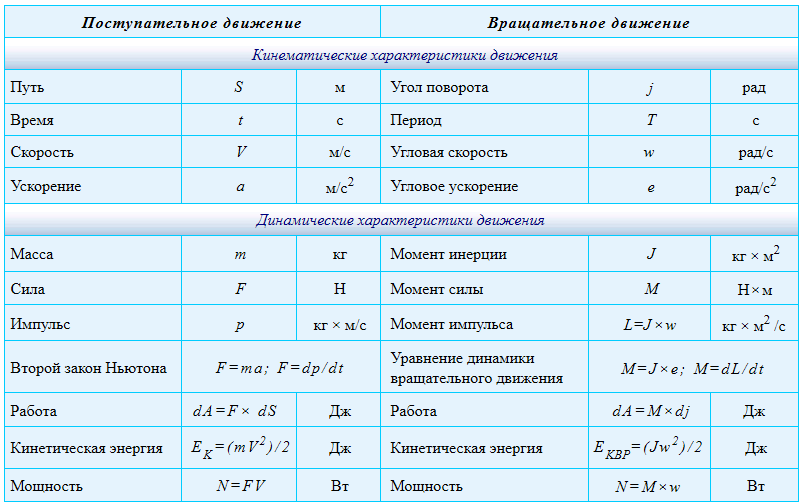
Аналогия величин и соотношений, характеризующих поступательное и вращательное движения