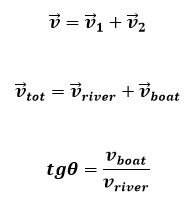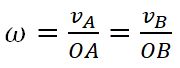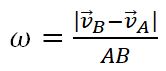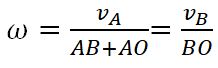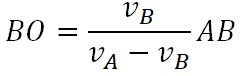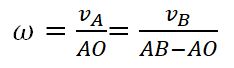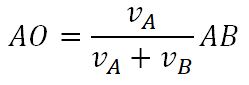Относительные кинематические понятия: траектория, координаты, перемещение, скорость.

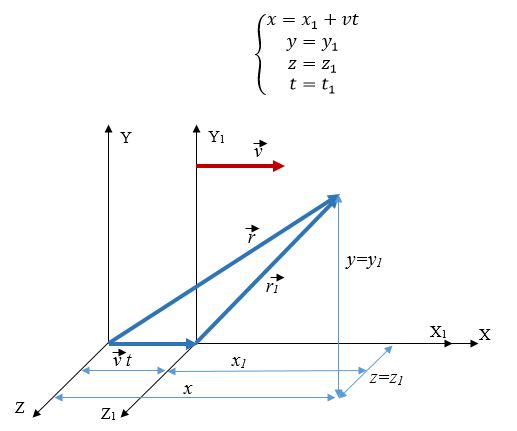
Преобразования Галилея

В случае движения системы отсчета (1) со скоростью v вдоль оси х относительно неподвижной системы отсчета:

Закон сложения скоростей

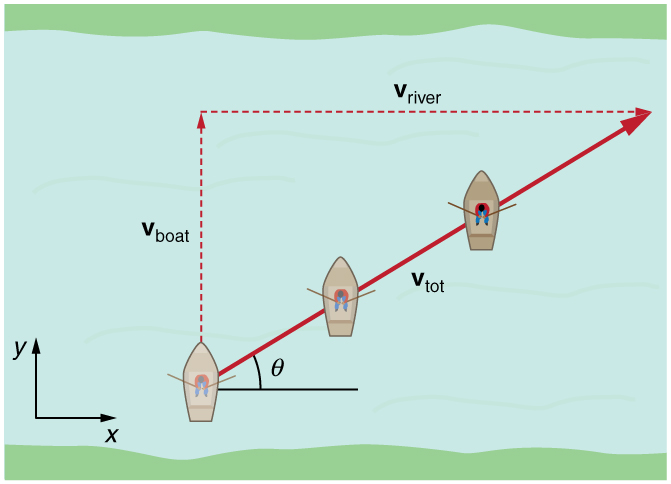
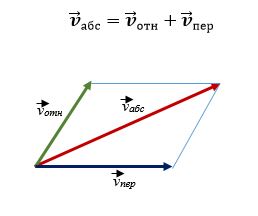
Абсолютная, относительная и переносная скорости

Движение относительно неподвижной системы координат называется абсолютным.

Движение относительно подвижной системы координат называется относительным.

Движение подвижной системы координат относительно неподвижной называется переносным.

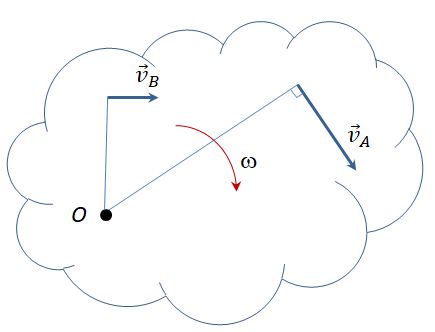
Мгновенный центр скоростей

При плоском движении в каждый момент времени существует единственная точка в плоскости движения, скорость которой равна нулю:

Свойства МЦС:

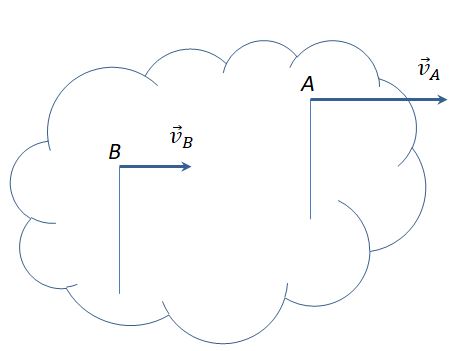
1. Для определения мгновенного центра скоростей надо знать только направления скоростей v_A и v_B каких-нибудьдвух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).

2. Для определения скорости любой точки плоской фигуры надо знать модуль и направление скорости какой-нибудьодной точки А фигуры и направление скорости другой ее точки В.

3. Угловая скорость ω плоской фигуры равна в каждый данный момент, времени отношению скорости какой-нибудьточки фигуры к ее расстоянию от мгновенного центра скоростей Р:

Или же угловая скорость ω плоской фигуры равна в каждый данный момент, времени отношению разности скоростей точек к расстоянию между ними

Способы нахождения мгновенного центра скоростей

 1. Известна скорость точки А и направление скорости точки В. МЦС находится на пересечении перпендикуляров к скоростям, проведённых в точках А и В.

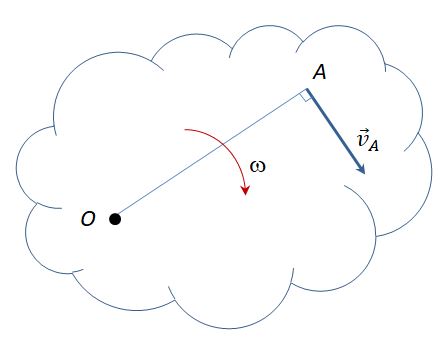
2. Известна скорость точки А тела и угловая скорость ω. МЦС находится на перпендикуляре к вектору v_A в точке А на расстоянии АO = v_A/ω.

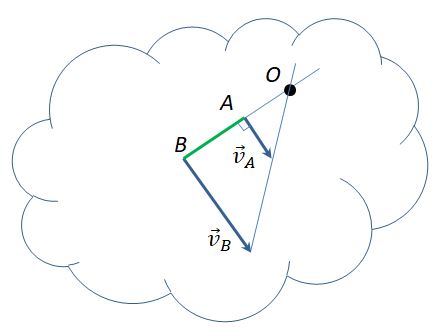
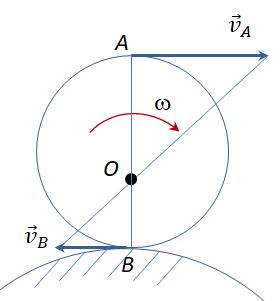
3. Известны длина отрезка АВ, скорости и двух точек тела  v_A и  v_В, которые перпендикулярны к отрезку АВ и направлены в одну сторону

МЦС находится на продолжении отрезка АВ в точке пересечения с прямой, проведенной через концы векторов и. Для определения составляем выражение

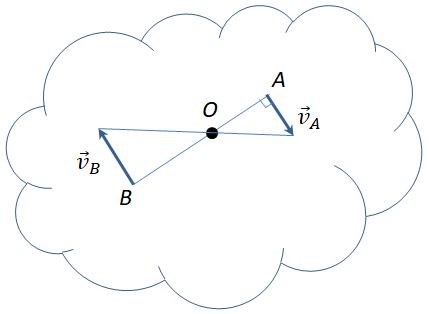
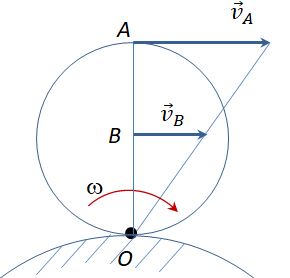
 4. Известны длина отрезка АВ, скорости v_A и  v_В двух точек тела, которые перпендикулярны отрезку АВ и направлены в разные стороны

МЦС находится внутри отрезка АВ. Для определения ω составляем выражение

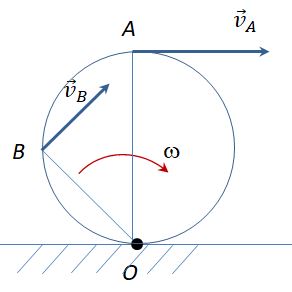
5. Тело перекатывается без проскальзывания по поверхности неподвижного тела. МЦС находится в точке соприкосновения тел в точке О

6. Тело перекатывается с проскальзыванием по поверхности неподвижного тела. МЦС находится в точке пересечения диаметра и линии, соединяющей концы векторов скорости О

7. Скорости двух точек тела параллельны. В этом случае МЦС находится в бесконечности, т.е. отсутствует. Тело совершает мгновенное поступательное движение, тогда скорости двух точек и всех других точек тела одинаковы, а их ускорения в общем случае могут быть разными