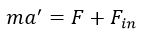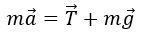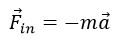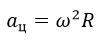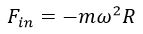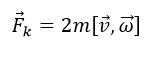Законы Ньютона применяются только для инерциальных систем отсчета. Но большинство реальных систем отсчета – неинерциальны. Оказывается, законы Ньютона можно применять и для неинериальных систем, если кроме сил, возникающих из-за воздействия тел друг на друга, добавить силы особого рода – силы инерции.

Тогда II закон Ньютона для неинерциальной системы отсчета запишется в виде:

где F– силы, возникающие из-за взаимодействия тел;
F_in– силы инерции, возникающие из-за неинерционности системы отсчета;
a’ – ускорение тела в неинерционной системе отсчета.

Силы инерции возникают из-за ускоренного движения системы отсчета, поэтому силы инерции возникают в следующих случаях:

1. ускоренное поступательное движение системы отсчета;
2. неподвижное тело во вращающейся системе отсчета;
3. движущееся тело во вращающейся системе отсчета.

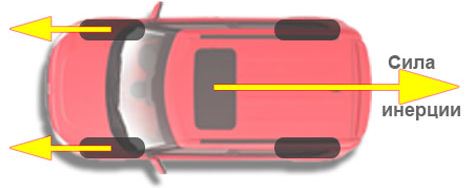
1. Силы инерции при ускоренном поступательном движении системы отсчета

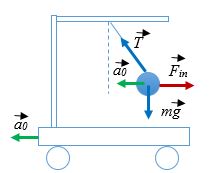
В движущейся с ускорением СО шарик, подвешенный на нити, отклоняется в сторону, противоположную ускорению. Это ускорение возникает из-за равнодействующей сил тяжести и упругости нити:

Но в СО, связанной с ускоренно движущимся телом, шарик покоится, что можно объяснить, введя силу инерции, создающую такое же, но противоположное по направлению ускорение:

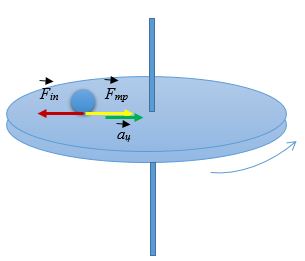
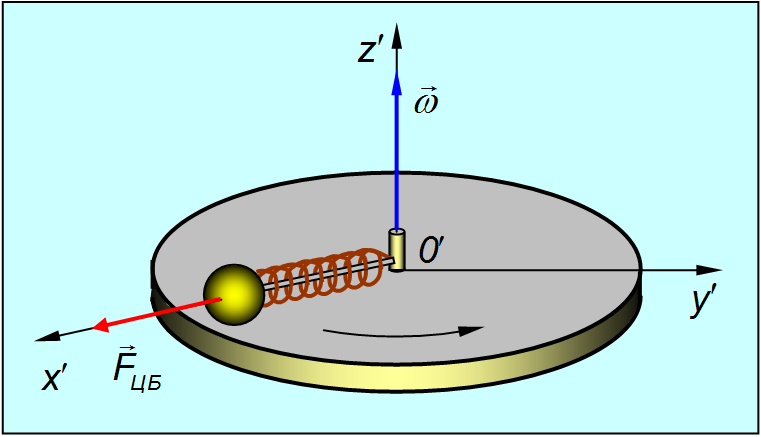
 2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета

При вращении тела в инерциальной СО силы, действующие на него, приводят к появлению центростремительного ускорения:

Во вращающейся системе отсчета тело может покоиться, если действующие на него силы, например, сила трения, компенсируется центробежной силой инерции.

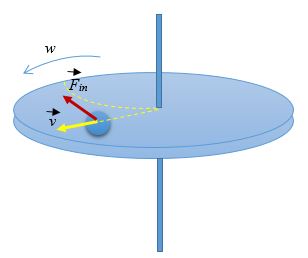
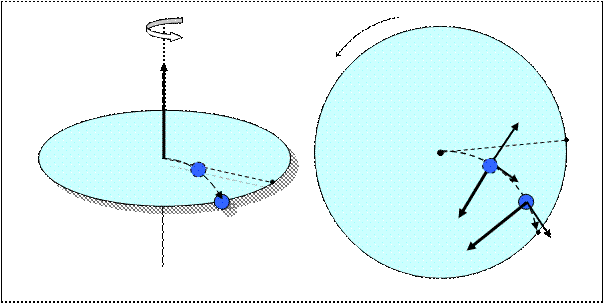
3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета

При движении тела по вращающемуся диску его траектория смещается:

Это возможно, если на тело действует сила инерции, направленная перпендикулярно скорости. Эта сила называется силой Кориолиса.