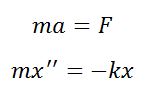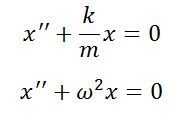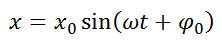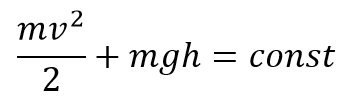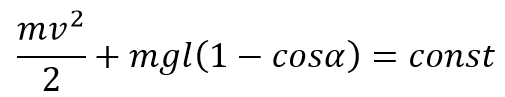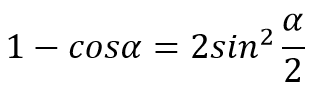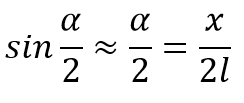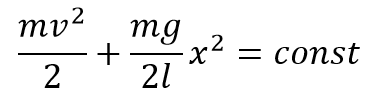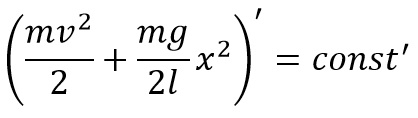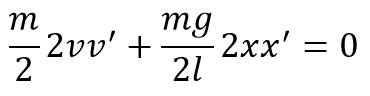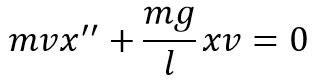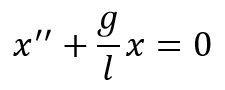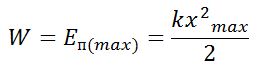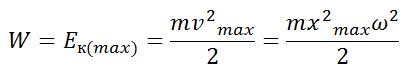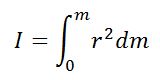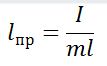Динамический метод По II закону Ньютона Дифференциальное уравнение свободных колебаний (однородное дифференциальное уравнение 2-го порядка)           Решение уравнения - формула вида x0 и φ0 - произвольные постоянные, определяемые из начальных условий

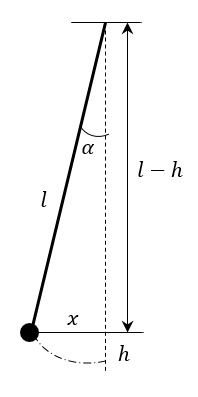
Энергетический метод Найдем полную механическую энергию маятника в произвольный момент времени: Из геометрии Поскольку угол малый, Тогда закон сохранения энергии примет вид: Найдем производную от обеих частей равенства: Уравнение гармонических колебаний

Энергетические превращения при гармонических колебаниях

Гармонические колебания происходят под действием упругой (квазиупругой) силы, являющейся консервативной, поэтому полная механическая энергия колебаний должна оставаться постоянной. в процессе происходит превращение кинетической энергии в потенциальную и обратно, причем в моменты наибольшего отклонения потенциальная энергия максимальна, а кинетическая равна нулю. 

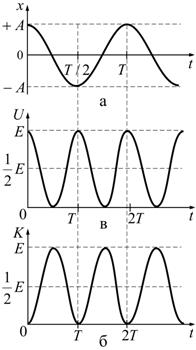Амплитуда потенциальной энергии Амплитуда кинетической энергии Частота изменения потенциальной и кинетической энергии в 2 раза выше частоты колебаний тела

Маятники

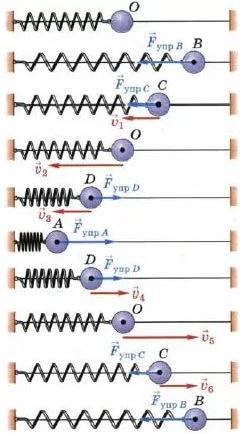
Пружинный маятник

Груз массой m, подвешенный на абсолютно упругой пружине k и совершающий гармонические колебания под действием силы упругости.

Идеализация модели:

• пружина невесома;
• груз абсолютно неупругий;
• в процессе колебаний выполняется закон Гука.

Период колебаний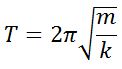
Циклическая частота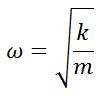
Уравнение движения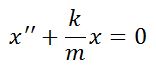

Математический маятник

Материальная точка, подвешенная на нерастяжимой нити, совершающая гармонические колебания под действием силы тяжести и силы упругости нити.

Идеализация модели:

• нить нерастяжима и невесома;
• тело не имеет размеров;
• вся масса сосредоточена в теле.

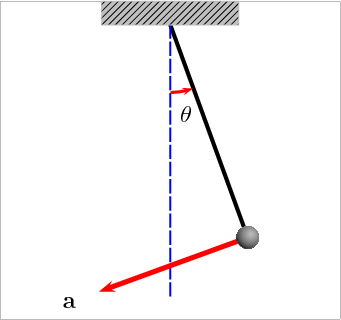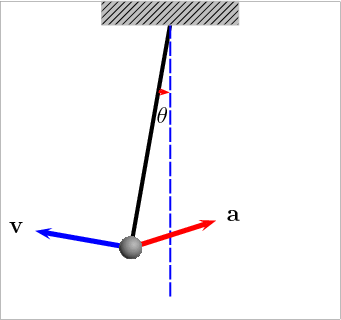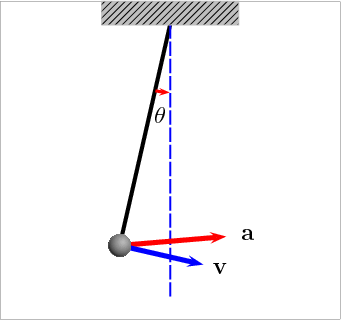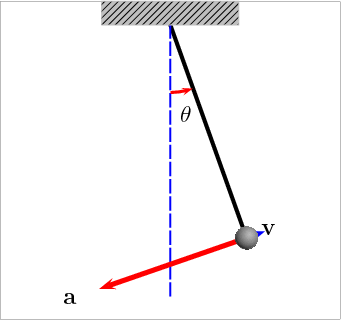
Период колебаний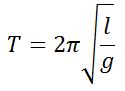
Циклическая частота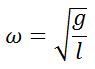
Уравнение движения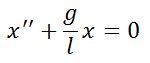

Физический маятник

Твердое тело, совершающее колебания около неподвижной горизонтальной оси подвеса,  не проходящей через центр масс, под действием силы тяжести.

Период колебаний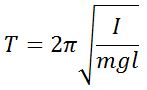
Циклическая частота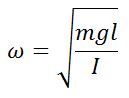
Уравнение движения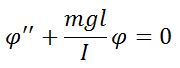

I - момент инерции тела. Если тело представляет собой совокупность точек с малыми массами, то момент инерции можно определить интегрированием: 

Величина l_пр называется приведенной длиной физического маятника, то есть длиной, которую имеет математический маятник, имеющий тот же период колебаний, что и данный физический маятник.