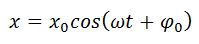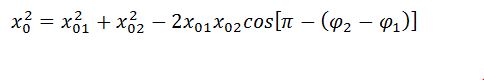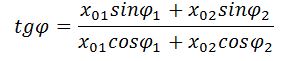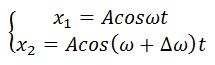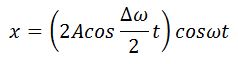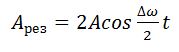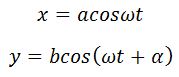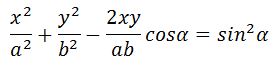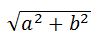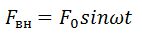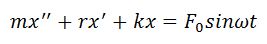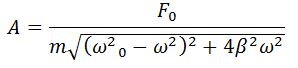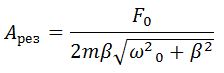Сложение нескольких гармонических колебаний становится наглядней, если изображать колебания в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой.
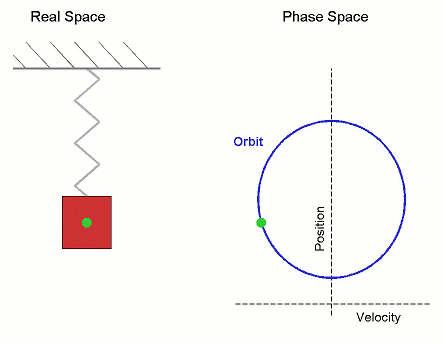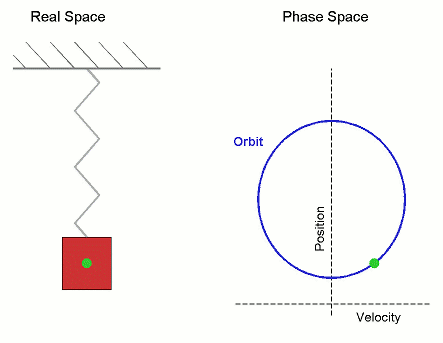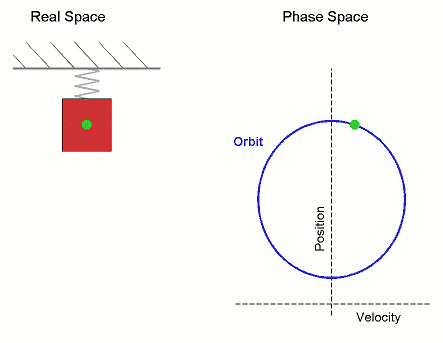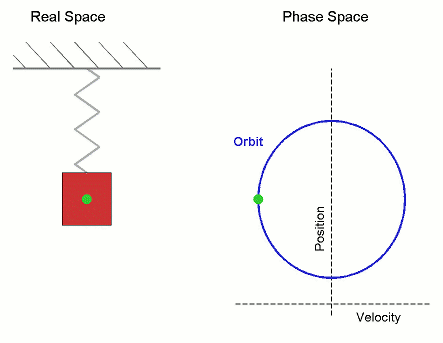
Тогда координата проекции вектора изменяется со временем по закону
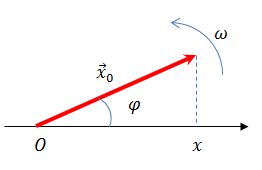
Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебаний, направление вектора образует с осью х угол, равный начальной фазе колебаний, а угловая скорость вращения вектора равна его циклической частоте.
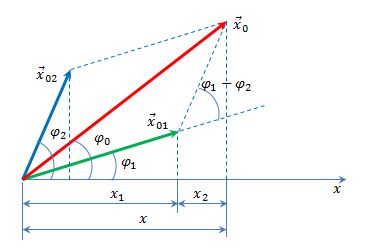
Сложение двух гармонических колебаний одинакового направления и одинаковой частоты
Смещение х колеблющегося тела будет равно сумме смещений х1 и х2:
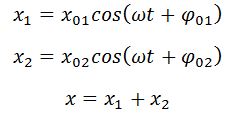
Вектор х0 представляет собой результирующую амплитуду колебаний. Он вращается с той же угловой скоростью ω и начальной фазой φ0.
Рассмотрим частные случаи.
- Если разность фаз φ1 - φ2 колебаний равна 0 (отличается на 2π), то амплитуда результирующего колебания равна сумме амплитуд: х = х1 + х2.
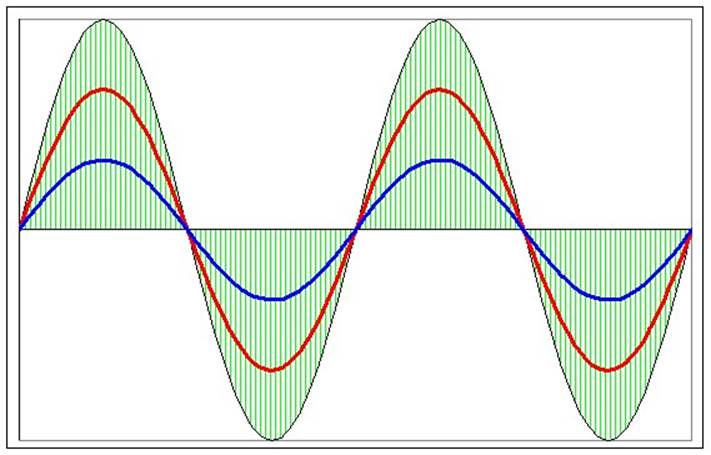
- Если оба колебания находятся в противофазе (разность фаз равна ±π), то результирующая амплитуда х = |х1 - х2|.
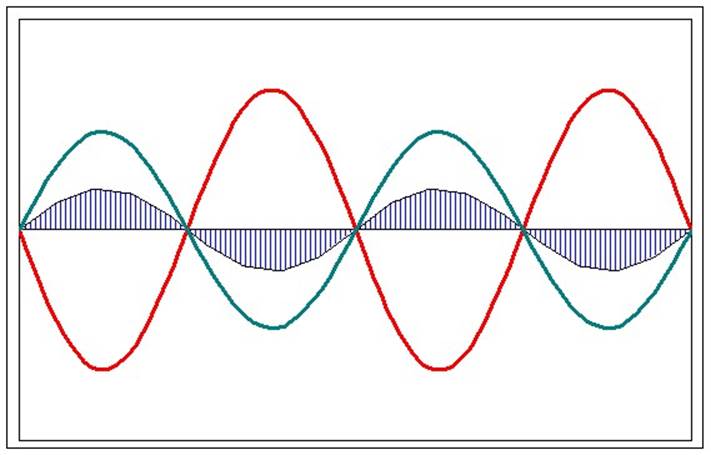
- Если частоты неодинаковы, то векторы будут вращаться с различной скоростью. Результирующий вектор пульсирует по величине и вращается с непостоянной скоростью.
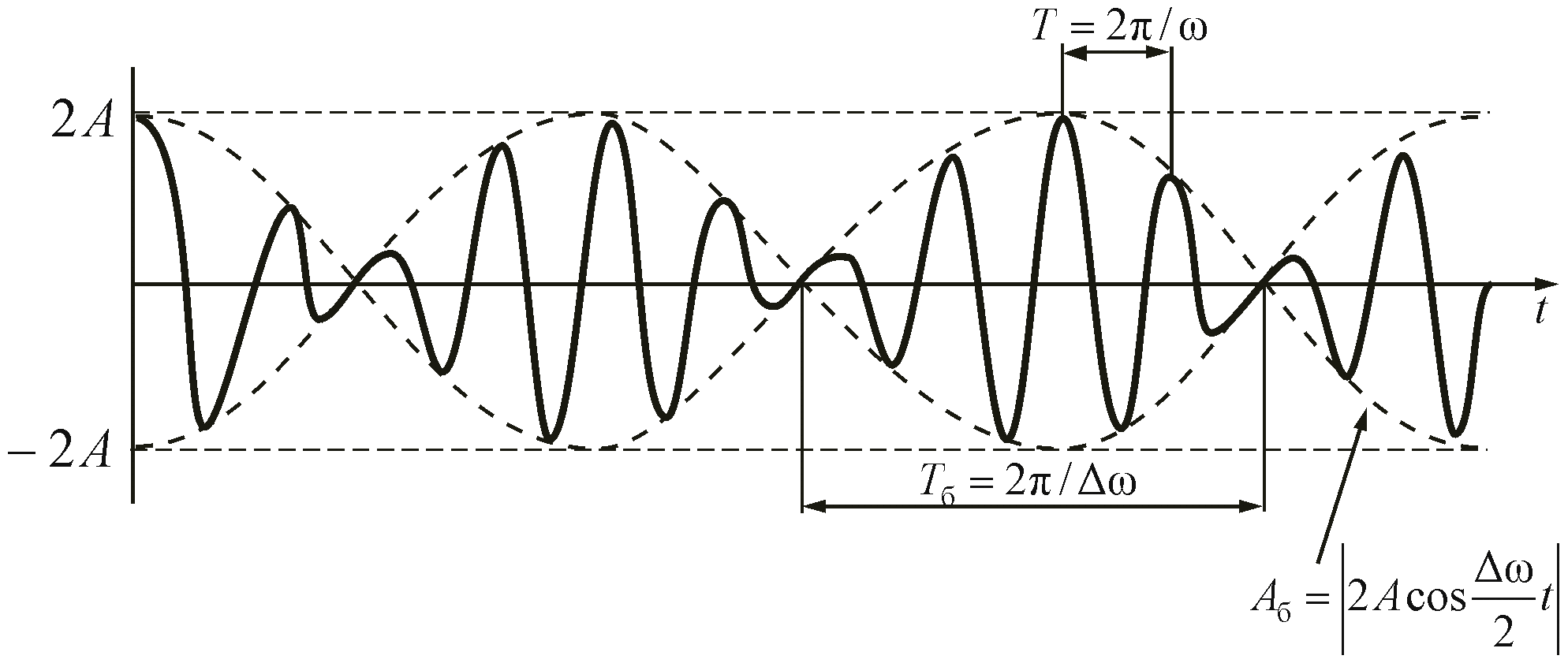
Биения
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.
Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
Тогда результирующее колебание можно представить в виде:
Амплитуда результирующего колебания меняется со временем по закону
Сложение взаимно перпендикулярных колебаний
Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.
Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:
где α - разность фаз обоих колебаний.
После преобразования получим уравнение траектории, которое представляет собой параметрическое уравнение эллипса, оси которого повернуты относительно осей х и у.
Рассмотрим частные случаи.
1. Разность фаз равна нулю. В этом случае получается уравнение прямой.
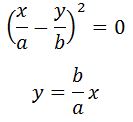
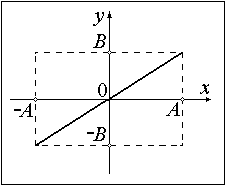
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой
2. Разность фаз равна ±π. Уравнение имеет вид прямой.
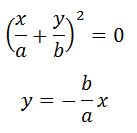
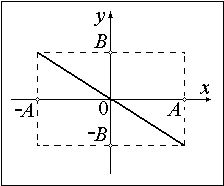
3. При α = ±π/2 получается уравнение эллипса, приведенного к координатным осям. При равенстве амплитуд эллипс превращается в окружность.
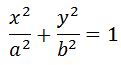
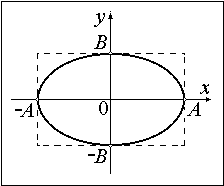
При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу. Чем ближе отношение частот к единице, тем сложнее получается фигура Лиссажу.
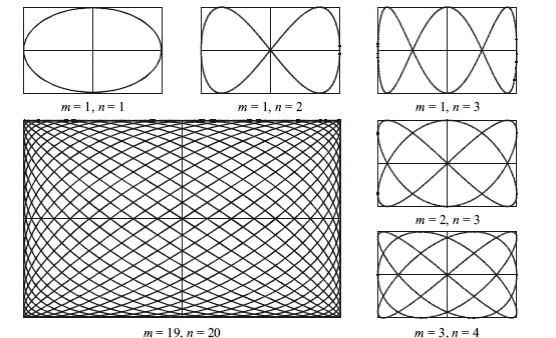
Резонанс
Резонанс - явление резкого возрастания амплитуды вынужденных колебаний при совпадении частот вынуждающей силы и собственных колебаний маятника. Вынужденные колебания происходят, если внешняя сила изменяется периодически:
Дифференциальное уравнение вынужденных колебаний
где Fтр = - rx'
Амплитуда колебания определяется формулой
где коэффициент затухания β = r/2m.
Для определения резонансной частоты надо найти минимум знаменателя. Резонансная амплитуда
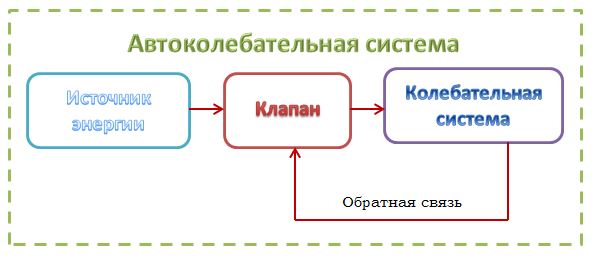
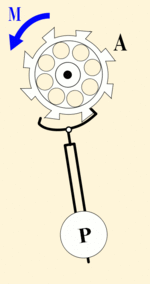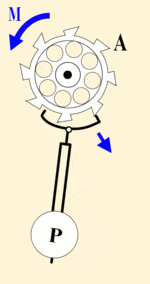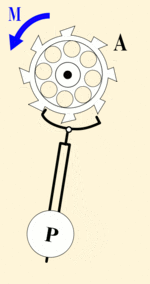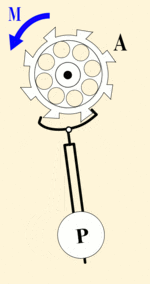
Автоколебания
При затухающих колебаниях энергия системы расходуется на преодоление сил сопротивления. Если восполнять эти потери, то колебания станут незатухающими. Если система сама управляет воздействием внешних сил, то такое колебательное движение называется автоколебанием.
В автоколебательной системе обязательно присутствуют элементы:
- сама колебательная ситема, ее параметры определяют частоту автоколебаний;
- источник энергии, поддерживающий автоколебания;
- клапан, регулирующий поступление энергии;
- механизм обратной связи, посредством которой система управляет клапаном так, чтобы поступающая энергия компенсировала потери за счет трения и сопротивления среды.
Примеры автоколебательных систем
|
Маятниковые часы |
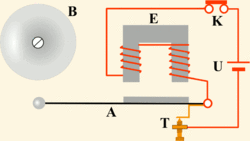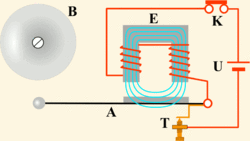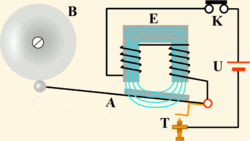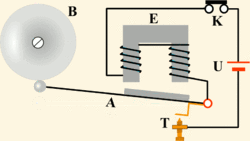
Электрический звонок
|
Биологические системы (сердце, легкие) |