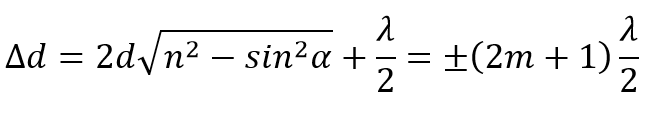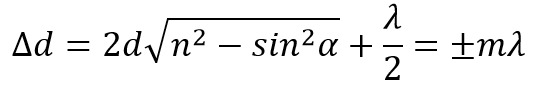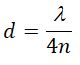Дисперсия света – это явление, обусловленное зависимостью показателя преломления n от частоты ν (длины волны λ) света

Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Первые экспериментальные наблюдения дисперсии света проводил в 1672 г. И. Ньютон. Он объяснил это явление различием масс корпускул.

Опыт Ньютона состоял в том, что узкий пучок солнечного света он направил на боковую грань трехгранной призмы, а при выходе пучка из противоположной боковой грани наблюдались разноцветные лучи в следующей последовательности – красный(К), оранжевый(О), желтый(Ж), зеленый(З), голубой(Г), синий(С), фиолетовый (Ф). Полученную им цветную полоску Ньютон назвал спектром.

 

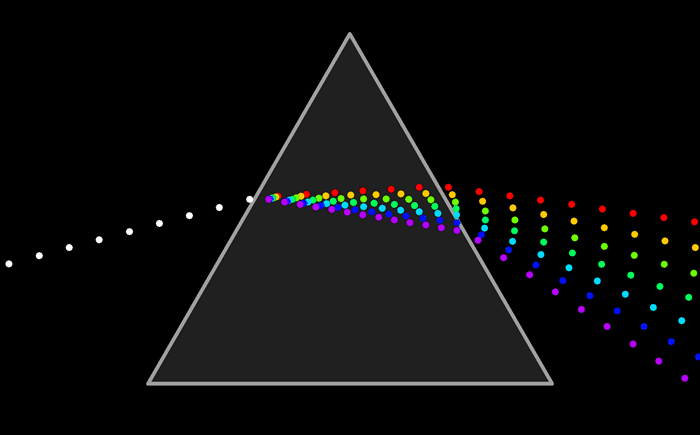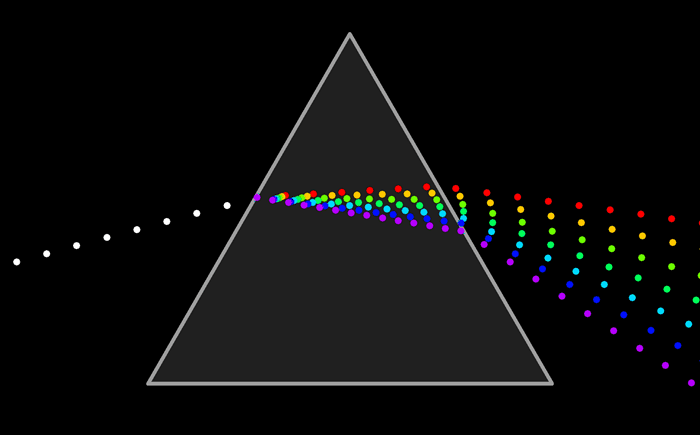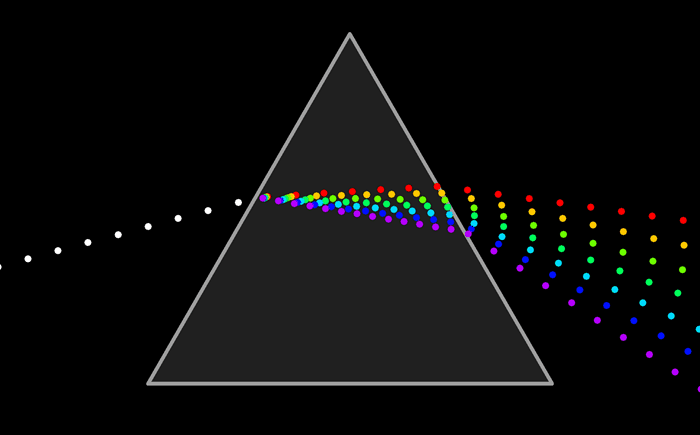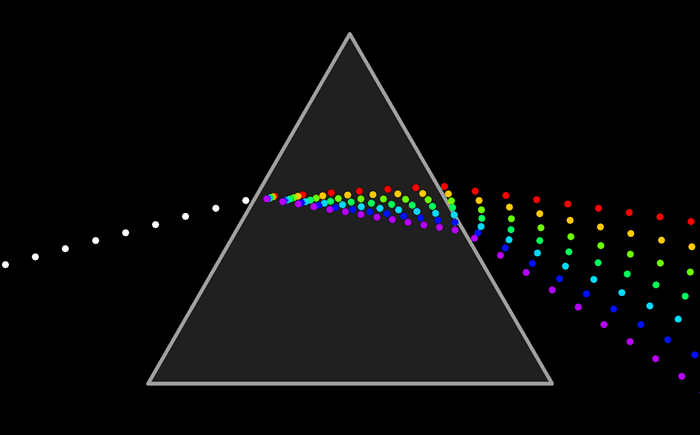
Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно, чем больше частота световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде:

• у света красного цвета фазовая скорость распространения в среде максимальна, а степень преломления — минимальна,
• у света фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна.

Цвет в природе

Говоря простым языком, цвет — это ощущение, которое получает человек при попадании ему в глаз световых лучей. 

Свет делится на излучаемый и отраженный. В физическом смысле оба вида света представляют собой две стадии одного и того же процесса, но их информационные роли существенно отличаются. В классическом случае излучаемый источником свет представляет собой максимально широкий спектр колебаний и кажется неокрашенным. Это чисто психологическое явление – нам удобнее воспринимать привычное солнечное освещение только в качестве ненавязчивого фона, а не сплошной и повсеместной радуги. 
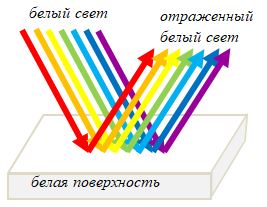
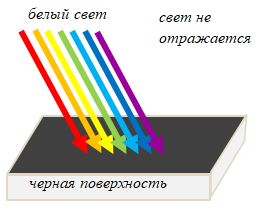
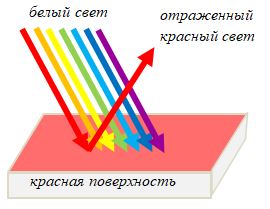
Зато отраженный свет изначально является основным источником зрительной информации, и мы максимально приспособлены именно к его восприятию. Поверхности предметов поглощают практически все падающее на них излучение, отражая только незначительную его часть. Чем ярче выражен цвет предмета, тем уже спектр его отражения: помидор отражает только красные лучи, апельсин – оранжевые и желтые, а бумага – почти весь падающий на нее свет. Поэтому помидор выглядит ярко-красным, апельсин – оранжевым, а бумага – просто белой. 

Излучаемый свет – в общем случае – это первичный свет, испускаемый источником света (солнцем, луной, светильниками и т.п.). Несмотря на то, что он является суммой множества составляющих, благодаря особенностям зрительного восприятия, излучаемый свет выглядит белым (или слегка тонированным). Соответственно, черный цвет представляет собой отсутствие света, или темноту. 
Отраженный свет – это вторичный (но отнюдь не второстепенный, а скорее наоборот, наиболее важный в информационном смысле) свет, идущий от поверхности неизлучающего объекта и содержащий информацию о нем, а не об источнике света. Именно благодаря отраженному свету мы видим предметы, которые его отражают. Он представляет собой разность, полученную при вычитании спектра поглощения объекта из спектра излучения светила. Белый цвет характеризует полное отражение падающего света, а черный – полное его поглощение. 

 

Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Это распределение называется интерференционной картиной.

 

Когерентными называются источники света одинаковой частоты, обеспечивающие постоянство разности фаз для волн, приходящих в данную точку пространства.

Интерференция света - сложение когерентных световых волн, в результате которого происходит пространственное перераспределение энергии, приводящее к образованию устойчивой картины их усиления или ослабления.

Опыт Юнга (1802 г.)

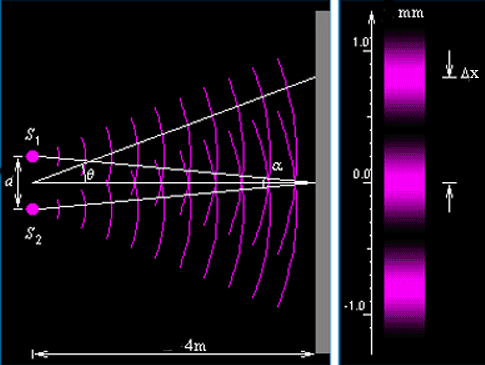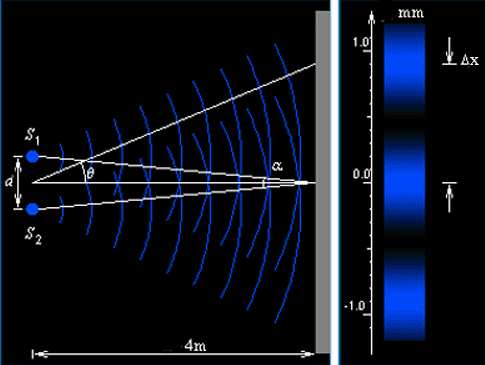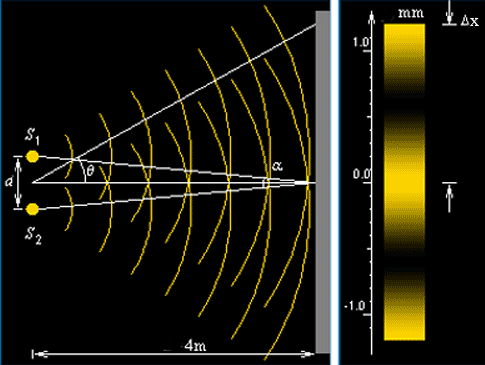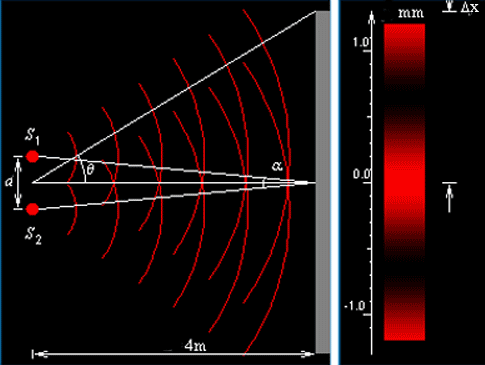
В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

Интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых 

Δd = mλ (m = 0, ±1, ±2, ...).

Интерференционный минимум (темная полоса) достигается при 

Δd = λ/2(2m + 1).

Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длины световых волн для разных цветов, хотя эти измерения и не были точными.

Зеркала Френеля

Свет от источника S падает расходящимся пучком на два плоских зеркала М₁ и М₂, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол α мал). Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S₁ и S₂ являющихся мнимыми изображениями S в зеркалах. Мнимые источники S₁ и S₂, взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рисунке она заштрихована). Интерференционная картина наблюдается на экране, защищенном от прямого попадания света заслон­кой

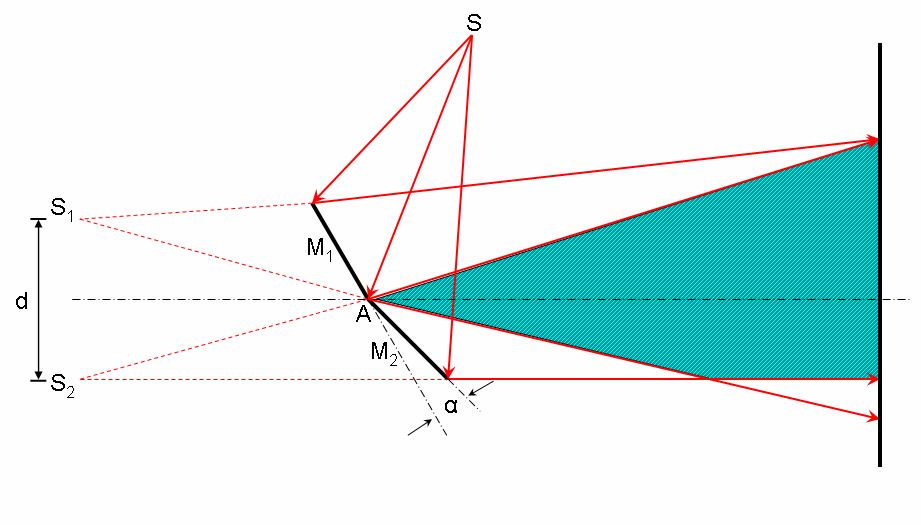
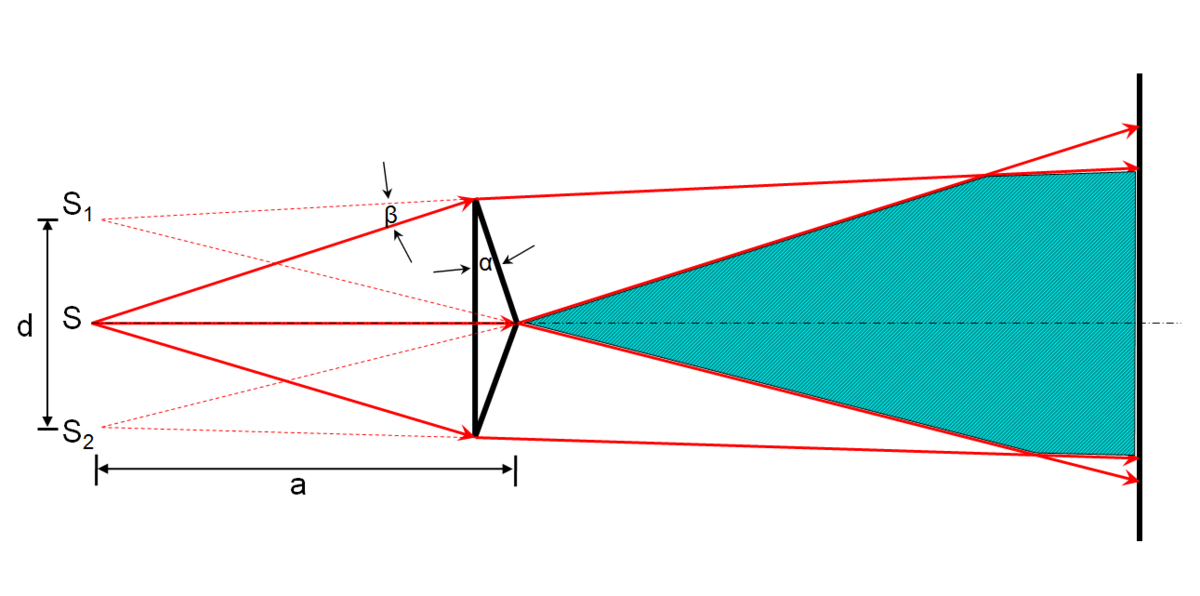
Бипризма Френеля

Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S₁ и S₂, являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.

Интерференция в тонких плёнках

Когда луч света проходит сквозь тонкую плёнку, часть его отражается от внешней поверхности, формируя первый луч, в то время как другая часть проникает внутрь плёнки и отражается от внутренней поверхности, образуя второй луч. Наблюдаемый в отражении цвет излучения определяется интерференцией этих двух лучей. Поскольку каждый проход света через плёнку создает сдвиг по фазе пропорциональный толщине плёнки и обратно пропорциональный длине волны, результат интерференции зависит от двух величин. Отражаясь, некоторые волны складываются в фазе, а другие в противофазе, и в результате белый свет, сталкивающийся с плёнкой, отражается с оттенком, зависящим от толщины плёнки. Эффект интерференции также зависит от угла, с которым луч света сталкивается с плёнкой.

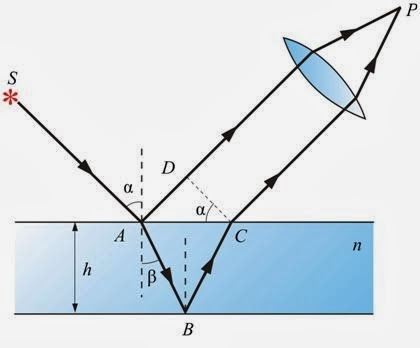
Пусть на плоскопараллельную, однородную, изотропную пластинку толщиной d падает под углом монохроматическая волна. За счет отражения её от нижней и верхней граней  происходит наложение образовавшихся когерентных волн в точке P. Разность хода волн

Δd = n (AB + BC) − (AD ± λ/2) = 2dn cos β ± λ/2.

Поправка λ/2 появляется потому, что свет в точке A отражается от оптически более плотной среды и при этом переходит в менее плотную.

Возникновение величины ±λ/2 объясняется потерей половины длины волны при отражении света от гарницы раздела сред. При n > n₀ половина волны будет потеряна в точке А, и при величине λ/2 будет стоять знак минус. Если n < n₀, то половина волны будет потеряна в точке В и при λ/2 будет стоять знак плюс.

При n > n₀ 

Δd = 2dn cos β + λ/2

 

Тогда условие интерференционного максимума в отраженном свете запишется следующим образом:

2dn cos β ± λ/2 = (2m + 1)λ/2

– если на разности хода интерферирующих волн укладывается нечетное число полуволн, то при наложении волны усиливают друг друга.

Условие интерференционного минимума в отраженном свете

2dn  cos β ± λ/2 = mλ

– если на разности хода интерферирующих волн укладывается четное число полуволн, то при наложении волны гасят друг друга.

На этой диаграмме изображены два луча красного света (лучи 1 и 2). Оба луча разбиваются на два, но нас интересуют только те части, которые изображены сплошными линиями. Рассмотрим луч, выходящий из точки Y. Он состоит из двух лучей, наложившихся один на другой: части луча 1, которая прошла через стенку пузыря и части луча 2, которая отразилась от внешней поверхности. Луч, прошедший через точки XOY путешествовал дольше луча 2. Допустим, случилось так, что длина XOY пропорциональна длине волны красного света, поэтому два луча складываются в фазе.

                         

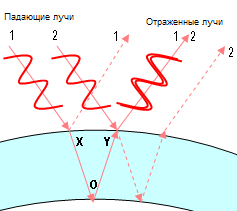
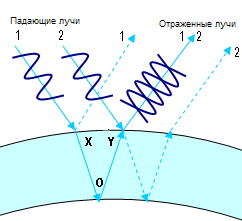
Эта диаграмма похожа на предыдущую, за исключением того, что длина волны света другая. В этот раз расстояние XOY непропорционально длине волны, и лучи складываются в противофазе. В результате, синий свет не отражается от пузыря с такой толщиной стенки.*

*https://ru.wikipedia.org/wiki/

На мыльную пленку, находящуюся в воздухе, падает по нормали пучок белого света. Определим, при какой наименьшей толщине d пленки отраженный свет с определенной длиной волны окажется максимально усиленным в результате интерференции.

Из условия интерференционного максимума находим для толщины пленки выражение

 Минимальное значение d получается при m = 0:

 

Если свет от двух когерентных источников распространяется в средах с разными показателями преломления, то оптическая разность хода определяется по формуле (s − путь в среде, n − показатель преломления среды):

Кольца Ньютона
И. Ньютон наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой.

Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла, называют кольцами Ньютона.

Они изучались Ньютоном при освещении как белым, так и монохроматическим светом.

                                         

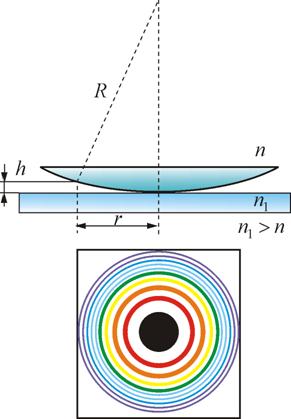
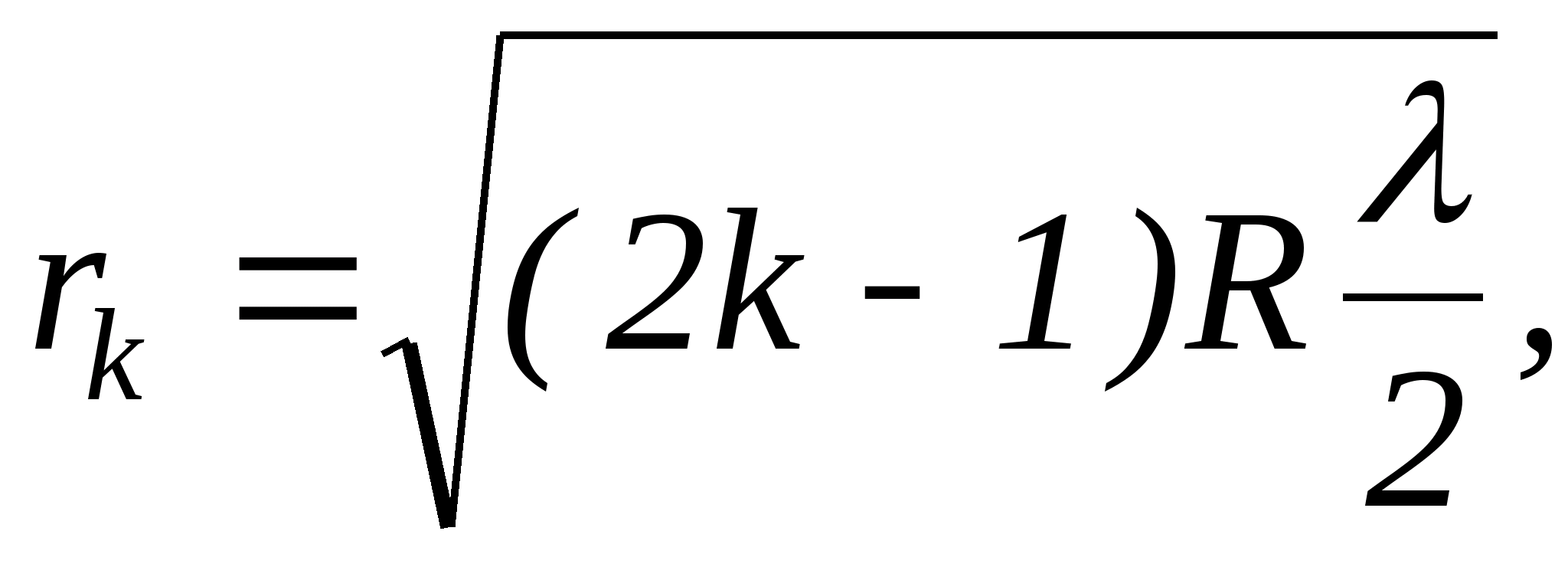
Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы R) определить λ, и, наоборот, по известной λ найти радиус кривизны линзы. Положение максимумов зависит от длины волны λ. Поэтому система светлых и темных полос наблюдается только при освещении монохроматическим светом. При наблюдении в белом свете интерференционная картина приобретает радужную окраску.

Применение интерференции
Просветление оптики

Интерференция при отражении от тонких пленок лежит в основе просветления оптики. Прохождение света через каждую преломляющую поверхность линзы сопровождается отражением примерно 4 % падающего света. В сложных объективах такие отражения совершаются многократно, и суммарная потеря светового потока достигает заметной величины. Отражения от поверхностей линз приводят к возникновению бликов. В просветленной оптике для устранения отражения света на каждую свободную поверхность линзы наносится тонкая пленка вещества с показателем преломления иным, чем у линзы. Толщина пленки подбирается так, чтобы волны, отраженные от обеих ее поверхностей, погашали друг друга. Особенно хороший результат достигается, если показатель преломления пленки равен корню квадратному из показателя преломления линзы. При этом условии интенсивность обеих отраженных от поверхностей пленки волн одинакова.

 

                                        

 

 

 

 

 

 

 

 

 

 

 

 

 

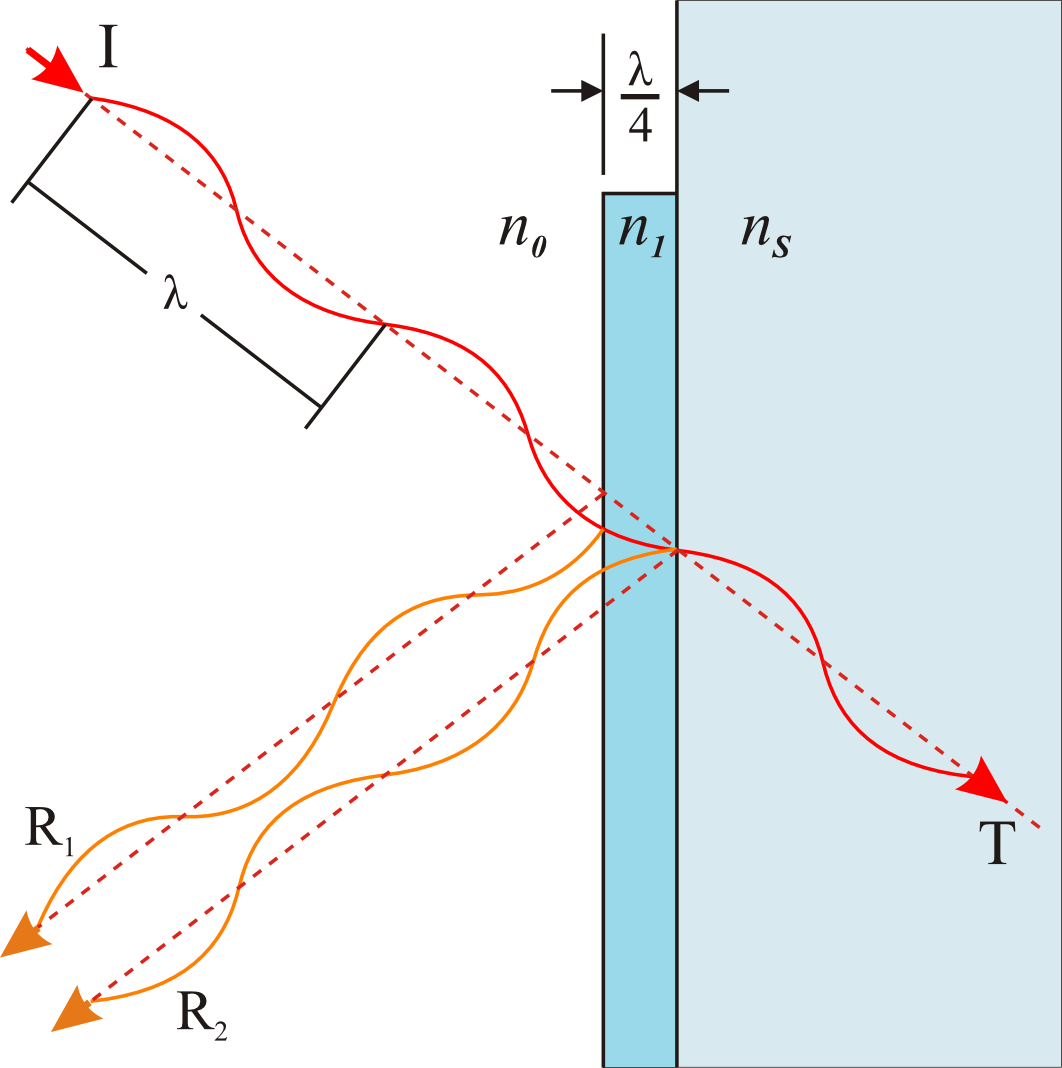
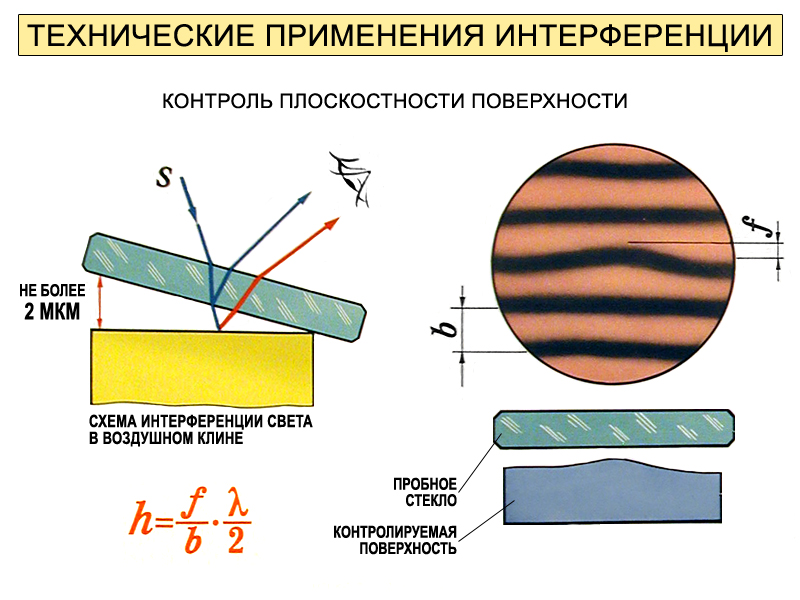
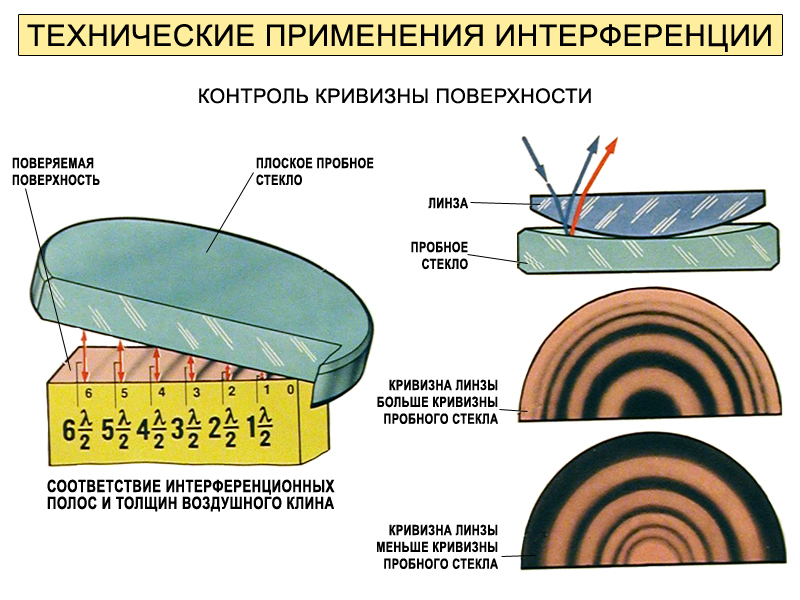
Технические применения интерференции