Специальная теория относительности

Первый постулат СТО — расширенный принцип относительности. Он уравнивал между собой не только инерциальные системы, движущиеся равномерно и прямолинейно друг относительно друга, но и распространил действие принципа на законы электродинамики.

Все физические явления протекают одинаковым образом во всех инерциальных системах отсчета; все законы природы и уравнения, их описывающие, инвариантны, т. е. не меняются, при переходе от одной инерциальной системы отсчета к другой.

Второй постулат утверждает, что скорость света в вакууме одинакова во всех ИСО. Таким образом, скорость света занимает особое положение в природе. В отличие от всех других скоростей, меняющихся при переходе от одной системы отсчета к другой, скорость света в пустоте является инвариантной величиной.

Скорость света в вакууме не зависит от движения источника света и одинакова во всех направлениях.

Следствия:

1) скорость света в вакууме является предельной: никакой сигнал, никакое воздействие одного тела на другое не могут распространяться со скоростью, превышающей скорость света в вакууме.

2) значение предельной скорости - скорости света в вакууме - должно быть одинаково во всех инерциальных системах отсчета: в противном случае эти системы можно было бы отличить друг от друга.

Преобразования Лоренца

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид: 

Следствия:

1) релятивистский эффект замедления времени 

Пусть, например, в некоторой точке x'системы K' происходит процесс длительностью τ₀ = t'₂ – t'₁ (собственное время), где t'₁ и t'₂ – показания часов в системе K' в начале и конце процесса. Длительность τ этого процесса в системе K будет равна 

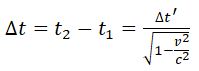
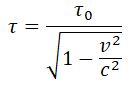
2) относительность одновременности

Пусть, например, в двух разных точках системы отсчета K' (x'₁ ≠ x'₂) одновременно с точки зрения наблюдателя в K' (t'₁ = t'₂ = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь 

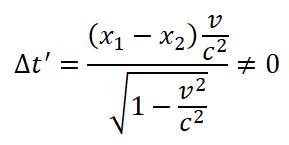
3) сокращение длины 

Разность между координатами конца и начала отрезка в системе отсчета, в которой он неподвижен, называется собственной длиной отрезка. В нашем случае l₀ = х₂' - х₁', где х₂' - координата конца отрезка в системе k' и х' - координата начала. Относительно системы k стержень движется. Длиной движущегося стержня принимают разность между координатами конца и начала стержня в один и тот же момент времени по часам системы k.

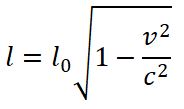
4) релятивистский закон сложения скоростей

Пусть, например, в системе отсчета K' вдоль оси x' движется частица со скоростью 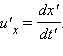 Составляющие скорости частицы u'_x и u'_z равны нулю. Скорость этой частицы в системе K будет равна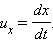 

С помощью операции дифференцирования из формул преобразований Лоренца можно найти: 

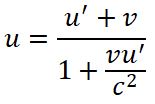
или в общем виде

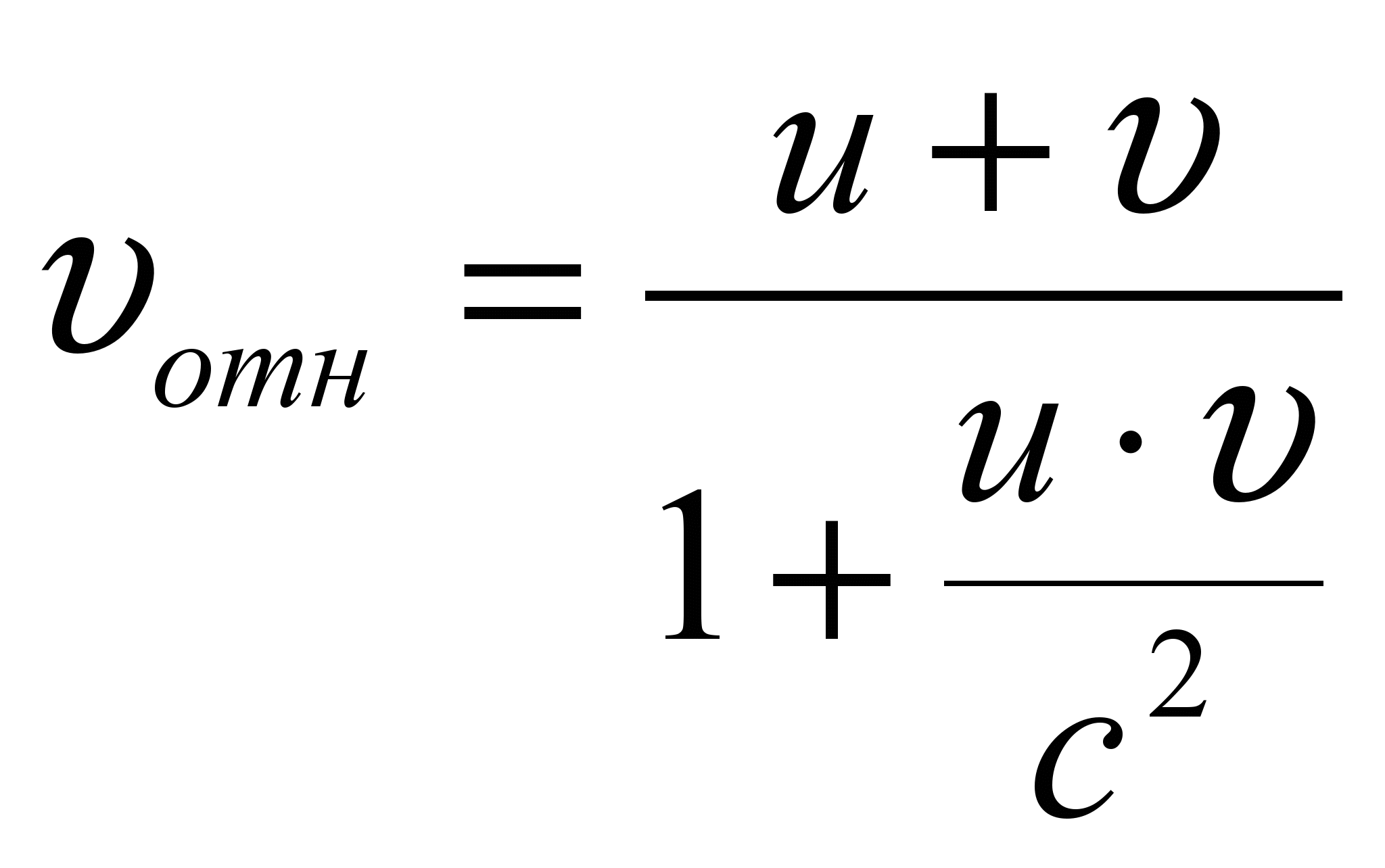
Замедление времени

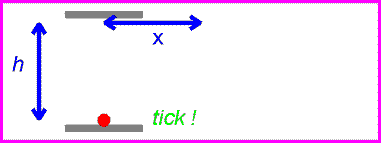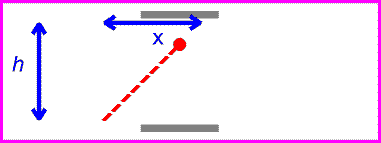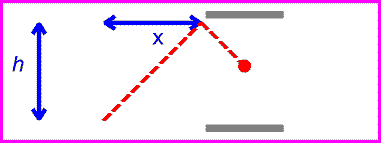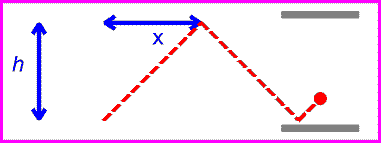
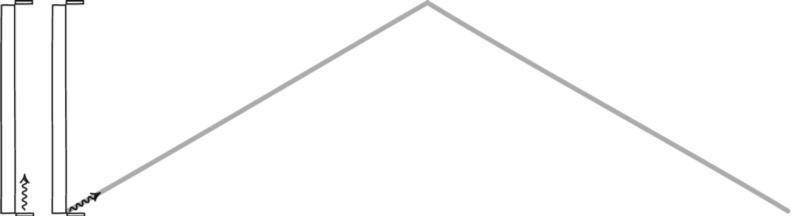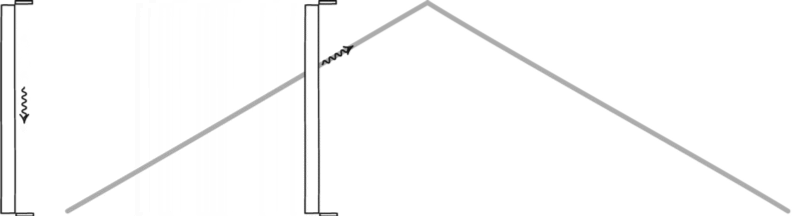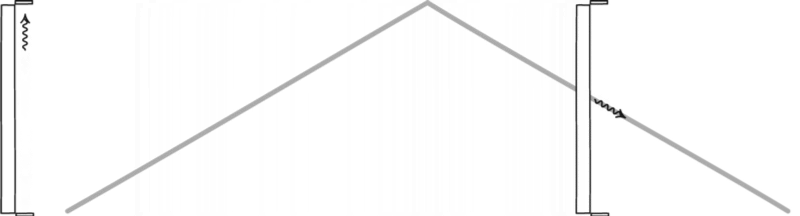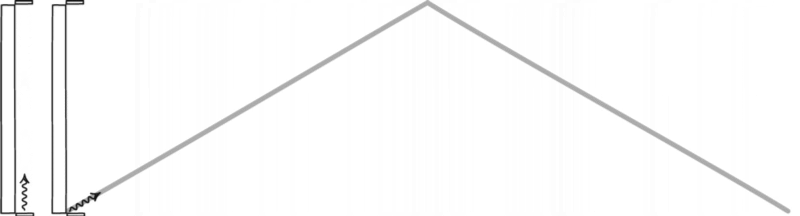
Световые часы измеряют время, отправляя луч света с нижней пластины на верхнюю пластину, где затем отражаются обратно на нижнюю пластину. Кажется, что световые часы являются лучшим измерителем времени, так как его скорость остается постоянной независимо от движения. 

Итак, на рис. 4 мы видим световые часы и обнаруживаем, что для перехода света снизу вверх и обратно требуется 1 с. Теперь посмотрим на рис. 5. В этом примере световые часы движутся вправо, но мы стоим на месте. Если бы мы увидели световой луч, когда часы проносились мимо нас, мы увидели бы, что луч проходит под углом к пластинам. 

Мы знаем, что часы, стоящие по-прежнему, посылают и получают сигнал с интервалом в 1 секунду. Мы также знаем, что скорость света постоянна. Независимо от того, где мы находимся, мы получили бы одинаковую скорость светового луча на рис. 4 и рис. 5. Но на рис. 5 видно, что свет перемещается дальше, потому что путь длиннее. Прошло больше времени, чтобы сделать один полный цикл отправки и получения, но скорость света не изменилась. Поскольку свет прошел дальше, это могло означать только то, что время, которое потребовалось, было большим. 

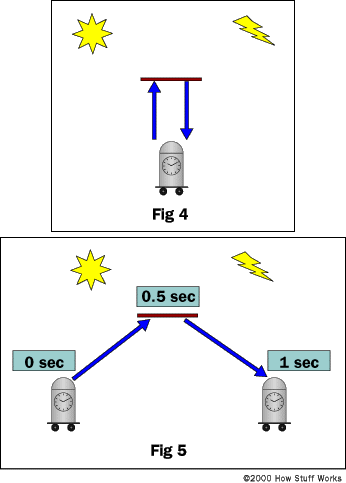
Тот факт, что скорость света одинакова во всех системах отсчета, является следствием того, что движущиеся часы работают медленно. Это означает, что если два события происходят в одном и том же месте, например, тики часов, движущийся наблюдатель будет измерять время между событиями дольше. Связь между временем, измеренным неподвижным наблюдателем Δt₀ и временем Δt, измеренным наблюдателем, движущимся со скоростью v, является:

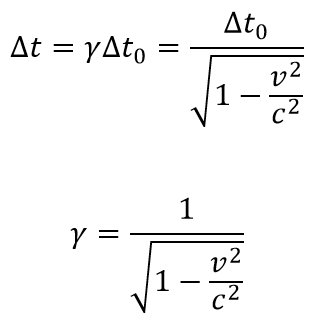
Константа пропорциональности γ называется фактором замедления времени. Она всегда больше единицы, но очень близка к нему при малых скоростях.

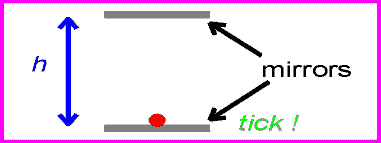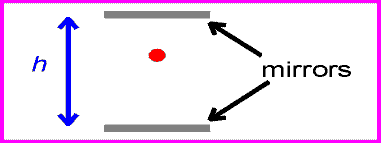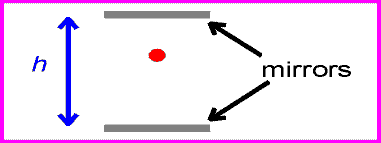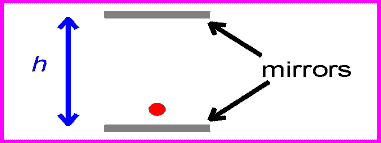
Время между тиками и стопами снова задается расстоянием, пройденным красным лучом, деленным на c .

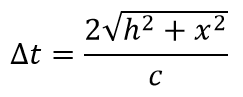
что больше, чем

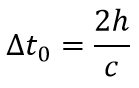
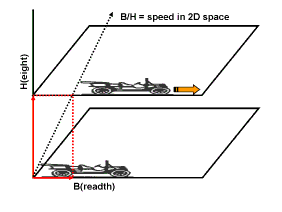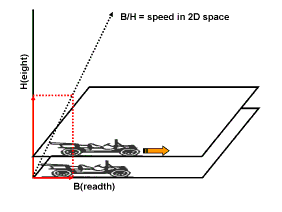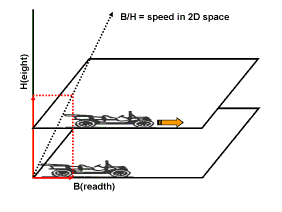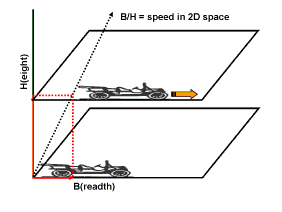
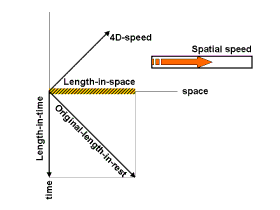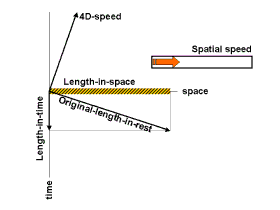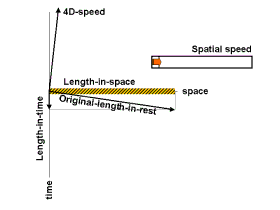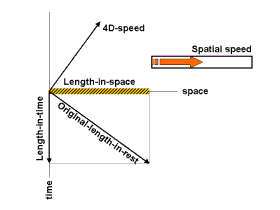
Парадокс близнецов

Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.

Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.

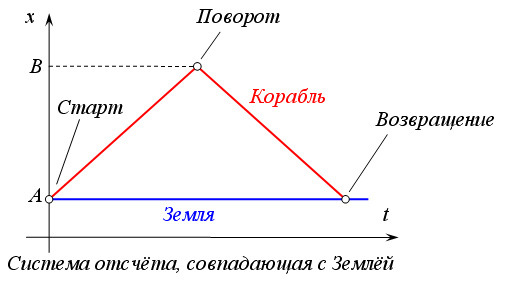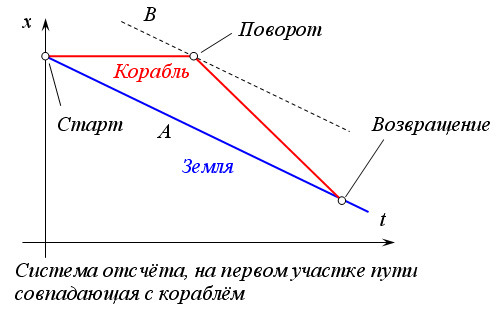Парадокс близнецов с точки зрения инерциальной системы отсчёта, связанной с Землёй	Парадокс близнецов с точки зрения инерциальной системы отсчёта,  на первой половине пути совпадающей c удаляющимся кораблём

Геометрическая интерпретация

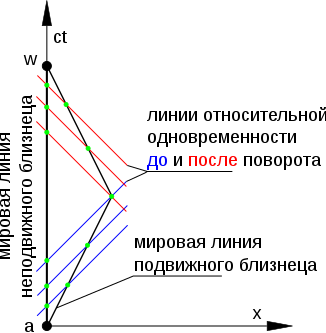
В пространстве Минковского мировая линия покоящегося (или двигающегося равномерно и прямолинейно) наблюдателя является отрезком прямой. Мировая линия путешественника, улетевшего с Земли и возвратившегося к ней, прямой не является (в простейшем случае мгновенного изменения скорости на противоположную в точке поворота она является ломаной, а при прохождении части пути с постоянным ускорением соответствующий участок линии будет дугой гиперболы). Так же как в обычной геометрии из всех линий, соединяющих две точки, самой короткой является прямая, так же и в пространстве Минковского из всех мировых линий, соединяющих две точки, самой длинной (а не самой короткой в силу псевдоевклидовости пространства-времени) является отрезок прямой.

Поскольку длина мировой линии наблюдателя, переместившегося в пространстве Минковского из точки a в точку w, с точностью до множителя c равна времени, которое было затрачено на это перемещение в его собственной системе отсчёта, мы имеем, что из всех наблюдателей, стартовавших в точке a и финишировавших в точке w, в системе отсчёта того наблюдателя, который покоился (или двигался равномерно и прямолинейно, если пространственные координаты точек a и w не совпадают), пройдёт наибольшее время.

Доказательство СТО

В 1935 году во вторичных космических лучах, рождающихся при столкновении первичных космических частиц с молекулами воздуха на высоте порядка 6 км были обнаружены новые элементарные частицы, получившие название мю-мезоны (мюоны). В лабораторных условиях удалось определить время их собственной жизни – порядка 2,2 мкс. Прожив столь малый промежуток времени, мю-мезоны распадаются на другие частицы. Продукты распада мю – мезонов, родившихся на высоте 6 км, обнаруживаются у Земли. Но возникала проблема: как за время жизни в 2,2 мкс, даже двигаясь со скоростью света с = 3·10⁸ м/с, мю-оны могут преодолеть расстояние в 6 км. Элементарный расчет давал лишь 300 м! (То, что распад происходил у поверхности Земли, было обнаружено экспериментально).

С точки зрения мюона он ощущает, что его время течёт нормально, но весь мир движется ему навстречу со скоростью в 99,9995% от световой. Кроме замедления времени мюон видит эффекты сокращения длины, то есть дистанция в 6 км, которую ему нужно пройти, кажется ему в 1000 раз меньшей, то есть, как 6 метров. И у него есть 86% шанс дойти до земли до того, как он распадётся, даже если считать с его точки зрения.