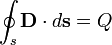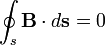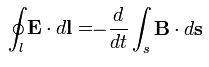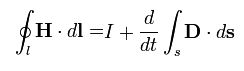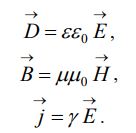Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь сэлектрическими зарядами и токами в вакууме и сплошных средах.

Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века. В 1820 году Ганс Христиан Эрстед обнаружил, что пропускаемый через провод гальванический ток заставляет отклоняться магнитную стрелку компаса. Это открытие привлекло широкое внимание учёных того времени. В том же 1820 году Био и Савар экспериментально нашли выражение для порождаемой током магнитной индукции (закон Био-Савара), и Андре Мари Ампер обнаружил, что взаимодействие на расстоянии возникает также между двумя проводниками, по которым пропускается ток. Ампер ввёл термин «электродинамический» и выдвинул гипотезу, что природный магнетизм связан с существованием в магните круговых токов.

Влияние тока на магнит, обнаруженное Эрстедом, привело Майкла Фарадея к идее о том, что должно существовать обратное влияние магнита на токи. После длительных экспериментов, в 1831 году, Фарадей открыл, что перемещающийся возле проводника магнит порождает в проводнике электрический ток. Это явление было названо электромагнитной индукцией. Фарадей ввёл понятие «поля сил» — некоторой среды, находящейся между зарядамии токами. Его рассуждения носили качественный характер, однако они оказали огромное влияние на исследования Максвелла.

Основу теории Максвелла составляют четыре структурных уравнения, которые записываются в интегральной и дифференциальной формах. В интегральной форме они выражают соотношения для мысленно проведенных в ЭМП контуров и замкнутых поверхностей, а в дифференциальной – показывают, как связаны между собой характеристики ЭМП и плотности электрических зарядов и токов в каждой точке пространства.

Дифференциальная форма

Уравнения Максвелла представляют собой в векторной записи систему из четырех уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейных дифференциальных уравнений в частных производных 1-го порядка для 12 компонент четырёх векторных функций (  ):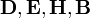

Название		СИ	Примерное словесное выражение
Закон Гаусса			Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля		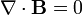	Не существует магнитных зарядов.
Закон индукции Фарадея			Изменение магнитной индукции порождает вихревое электрическое поле.
Теорема о циркуляции магнитного поля		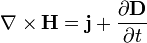	Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

 — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

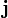 — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае - случае тока, порождаемого одним типом носителей заряда, она выражается просто как  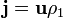, где 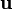 — (средняя) скорость движения этих носителей в окрестности данной точки, ρ₁ - плотность заряда этого типа носителей (она в общем случае не совпадает с ρ); в общем случае это выражение надо усреднить по разным типам носителей;

 — скорость света в вакууме (299 792 458 м/с);

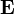 — напряжённость электрического поля (в единицах СИ — В/м);

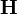 — напряжённость магнитного поля (в единицах СИ — А/м);

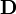 — электрическая индукция (в единицах СИ — Кл/м²);

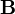 — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с⁻²•А⁻¹);

 — дифференциальный оператор набла, при этом:

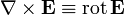 означает ротор вектора,

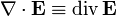 означает дивергенцию вектора.

Интегральная форма

При помощи формул Остроградского-Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:

Название		СИ	Примерное словесное выражение
Закон Гаусса			Поток электрической индукции через замкнутую поверхность sпропорционален величине свободного заряда, находящегося в объёме v, который окружает поверхность s.
Закон Гаусса для магнитного поля			Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).
Закон индукции Фарадея			Изменение потока магнитной индукции, проходящего через незамкнутую поверхностьs, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре l, который является границей поверхности s.
Теорема о циркуляции магнитного поля			Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность s, пропорциональны циркуляции магнитного поля на замкнутом контуре l, который является границей поверхности s.

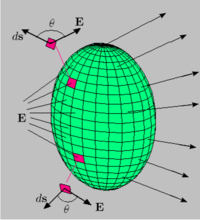
Введённые обозначения:

 — двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём 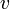 , и открытая поверхность в случае законов Фарадея и Ампера-Максвелла (её границей является замкнутый контур  ).

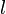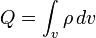  — электрический заряд, заключённый в объёме  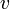, ограниченном поверхностью  (в единицах СИ — Кл);

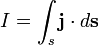  — электрический ток, проходящий через поверхность  (в единицах СИ — А).

При интегрировании по замкнутой поверхности вектор элемента площади  направлен из объёма наружу. Ориентация  при интегрировании по незамкнутой поверхности определяется направлениемправого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по  .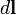

Полная система уравнений Максвелла для электромагнитных полей

Данные четыре структурных уравнения дополняются тремя материальными уравнениями, характеризующими свойства среды. Для изотропных несегнетоэлектрических и неферромагнитных сред материальные уравнения имеют вид, соответственно